Quiz frågor om derivata och kontinuitet

Hej!
Jag förstår inte varför mitt svar är felaktigt här. i första frågan ser det ut som att d/dx är ju -2x^-3*f'(x)?
destiny99 skrev:
Hej!
Jag förstår inte varför mina svar är felaktiga här. i första frågan ser det ut som att d/dx är ju -2x^-3*f'(x)? Den andra misstänker jag handlar om satsen om mellanliggande värden
För den andra frågan så inser du svaret så fort du har ritat upp funktionen. Om du mot förmodan inte gör det: Lägg upp din graf här.
Gör en separat tråd för den första frågan, det blir så rörigt om man har mer än en fråga per tråd.
Smaragdalena skrev:destiny99 skrev:
Hej!
Jag förstår inte varför mina svar är felaktiga här. i första frågan ser det ut som att d/dx är ju -2x^-3*f'(x)? Den andra misstänker jag handlar om satsen om mellanliggande värden
För den andra frågan så inser du svaret så fort du har ritat upp funktionen. Om du mot förmodan inte gör det: Lägg upp din graf här.
Gör en separat tråd för den första frågan, det blir så rörigt om man har mer än en fråga per tråd.
Hm
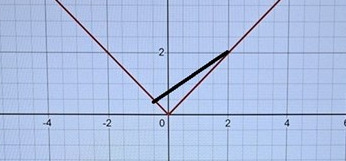
Om man deriverar |x| så är den ju x och -x beroende på om x>0 samt x<0. Om man väljer någon godtycklig tal mellan [-1/2,2] mellan de blåa linjerna tex x =1 så ser vi att derivatan är inte lika dvs f'(1)=1 och f'(1)=-1.

Finns det någonstans där funktionen har samma lutning som den svarta linjen?
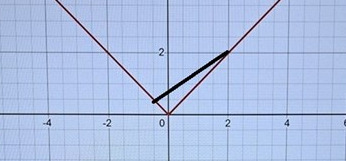
Smaragdalena skrev:Finns det någonstans där funktionen har samma lutning som den svarta linjen?
Nej jag kan inte hitta det. Se min uppdaterad inlägg i #3
Alltså är påståendet falskt.
Smaragdalena skrev:Alltså är påståendet falskt.
Aa
Rensat bort den andra frågan i citaten för en renare tråd. /moderator