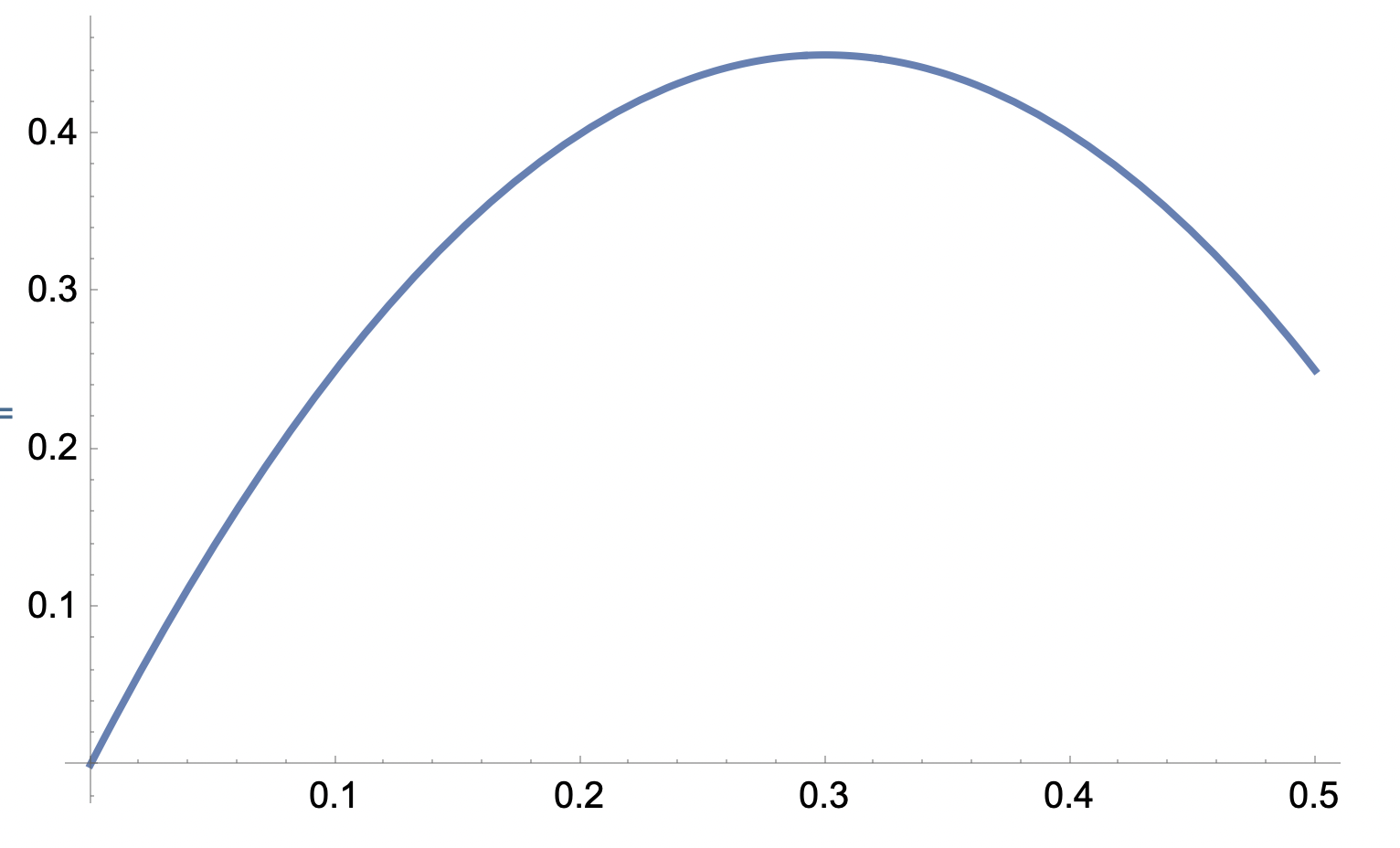
Punkt längst från origo på en parabel
Hej,
Jag behöver hjälp med en fråga som lyder:
"Vi undersöker parabeln y=3x-5x² då 0≤x≤1/2. Vilken punkt på denna båge är längst från origo?Algebraisk lösning krävs för full poäng."
Jag deriverade funktionen och beräknade dess nollställe vilket blev 0,3 och fick därför koordinaterna (0,3;0,45) för punkten. I facit är svaret (0,4;0,4). Jag förstår inte hur man får fram det svaret.
All hjälp uppskattas!
Du skall inte derivera y(x). y(x) är kurvan på vilken punkten ligger.
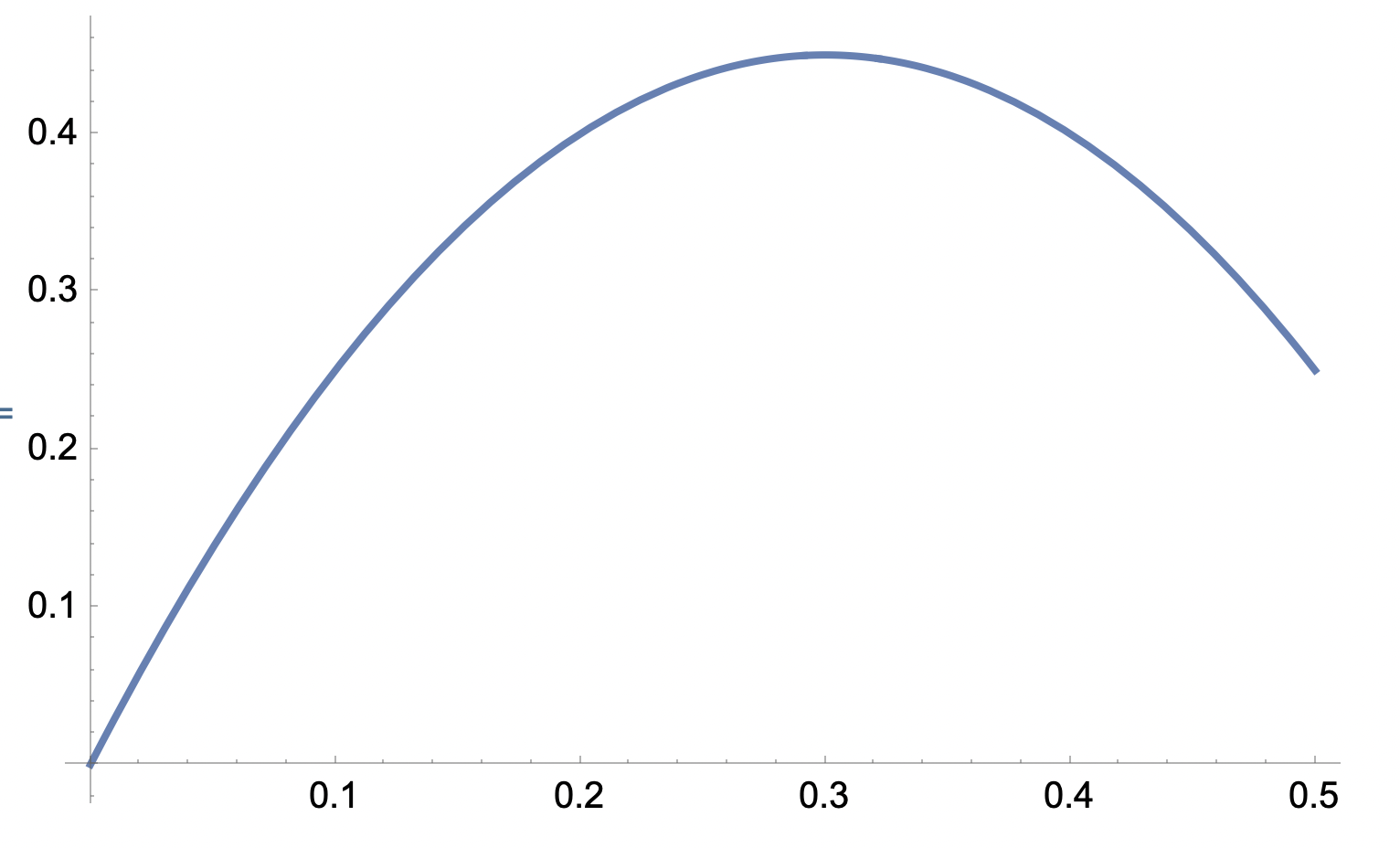
Sätt ut en godtycklig punkt (x,y) på kurvan och dra en rät linje till origo. Det är detta avstånd som skall maximeras.
Beräkna avståndet m.h.a. Pythagoras' sats eller avståndsformeln.
Notera att maximera avståndet är detsamma som att maximera det kvadratiska avståndet, vilket ger enklare räkningar.
Prova och räkna lite och återkom om det inte löser sig.
Trinity2 skrev:Du skall inte derivera y(x). y(x) är kurvan på vilken punkten ligger.
Sätt ut en godtycklig punkt (x,y) på kurvan och dra en rät linje till origo. Det är detta avstånd som skall maximeras.
Beräkna avståndet m.h.a. Pythagoras' sats eller avståndsformeln.
Notera att maximera avståndet är detsamma som att maximera det kvadratiska avståndet, vilket ger enklare räkningar.
Prova och räkna lite och återkom om det inte löser sig.
Tack så mycket, jag lyckades lösa den :)