Proton som rör sig i ett elektriskt fält
Hej,
Jag behöver hjälp med följande uppgift:
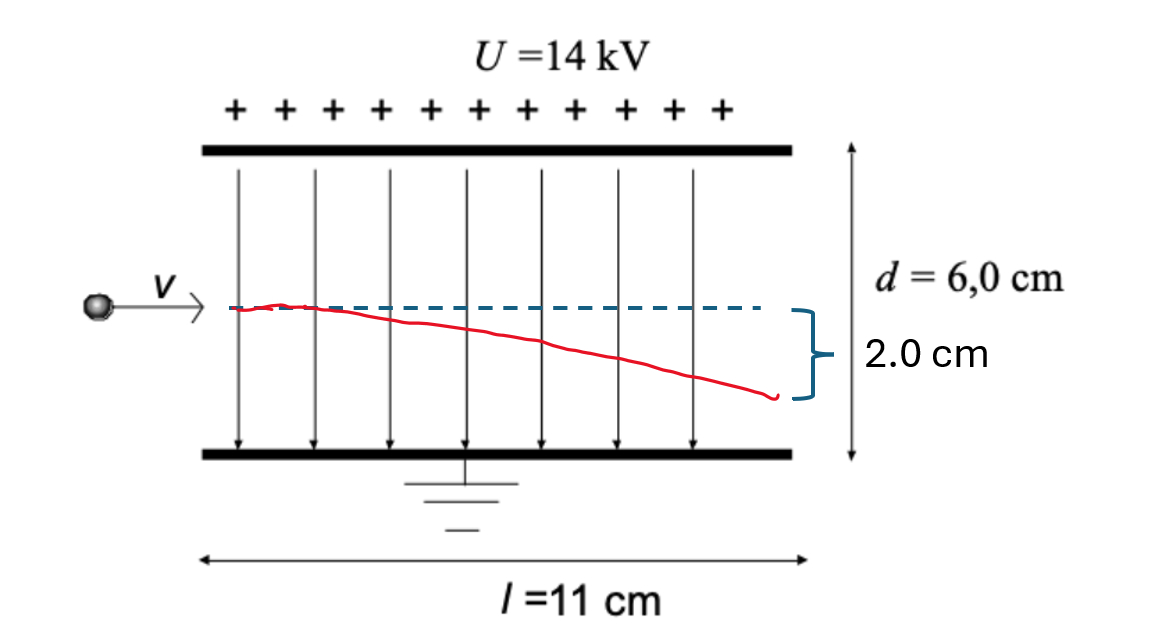
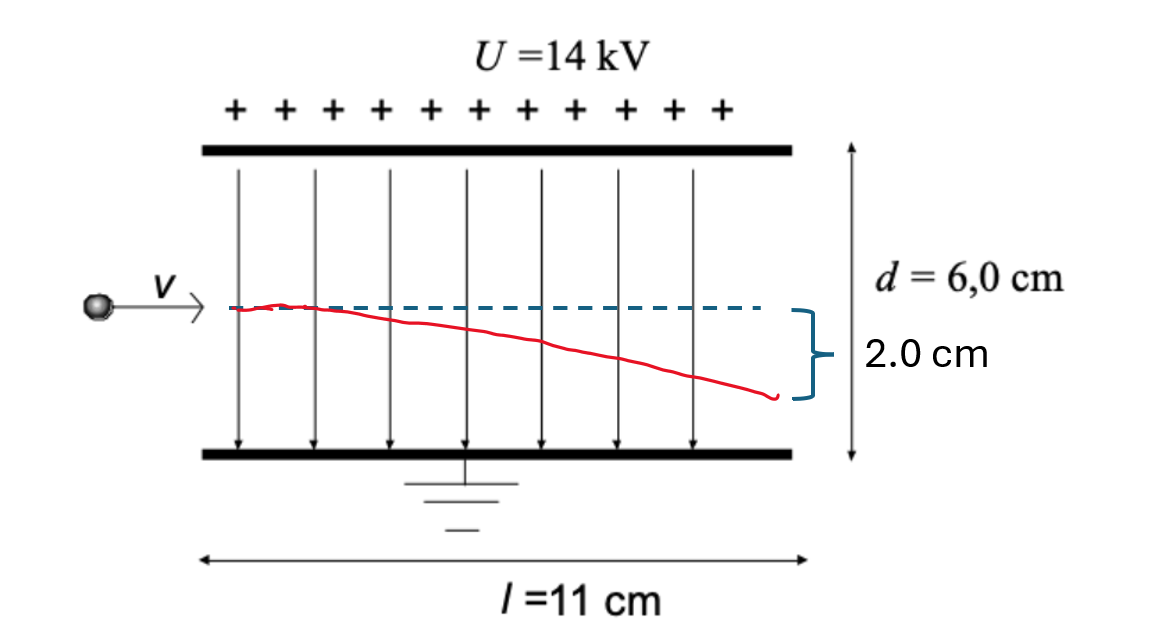
Bilden visar en proton som rör sig in i ett elektriskt fält. Genomför lämpliga beräkningar för att svara på följande frågor:
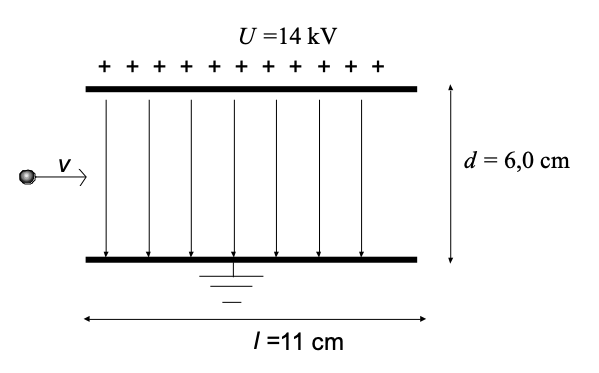
a. Om protonen lyckas komma igenom fältet, vart kommer partikeln vara i förhållande till när den kom in? Om partikeln har hastigheten 2,5 Mm/s. när den åker in i fältet?
b. Hur skulle resultatet förändras om det istället vore en elektron?
Såhär har jag tänkt när det gäller a uppgiften:
Om protonen lyckas komma igenom fältet så kommer den påverkas av en elektrisk kraft. För att få fram kraften så behöver man beräkna den elektriska fältstyrkan:
E = U/d = (14 * 10³)/(0,06) ≈ 2,33 * 10⁵ V/m
Nu kan den elektriska kraften beräknas: F = E*q = 2,33 * 10⁵ * 1,6 * 10^19 ≈ 3,7 * 10^-14 C
Vad är nästa steg? Jag tänker att man behöver beräkna accelerationen. Men påverkas laddningen alltid av en acceleration när den befinner sig i ett elektrisk fält, eller är det endast om det finns en nettokraft? Hur vet man om det finns en nettokraft i denna situation? Om det nu finns en acceleration, så blir det väl endast i vertikal led, då inga nettokrafter verkar i horisontell led.
ay = F/m = E*q/m = (3,7 * 10^-14)/(1,67 * 10^-27) ≈ 2,2 * 10^13 m/s²
Nästa steg är väl att beräkna läget. Eftersom det är en proton så vill den röra sig till minus plattan. Så endast sträckan i y-led ska beräknas (?).
sy = v0 * t - gt²/2
Vad blir då v0? Hastigheten som anges?
Tiden kan väl räknas ut genom t = s/v där s är sträckan i x-led, dvs. 0,11 m, och v är hastigheten i x-led.
Tänker jag rätt så länge?
Tack på förhand :)
Hej!
Du kan tänka dig att den laddade partikeln i det elektriska fältet påverkas av en kraft, på samma sätt som en massa påverkas av en kraft när den befinner sig i ett gravitationsfält.
Förstår du lättare då? Du är på helt rätt väg!
Vad är v0y i rörelsen?
.
JohanF skrev:Hej!
Du kan tänka dig att den laddade partikeln i det elektriska fältet påverkas av en kraft, på samma sätt som en massa påverkas av en kraft när den befinner sig i ett gravitationsfält.
Förstår du lättare då? Du är på helt rätt väg!
Vad är v0y i rörelsen?
.
Är det en nettokraft? Hur vet jag det isåfall? v0y behöver väl beräknas, eftersom hastigheten som anges är i x-led. Men hur gör jag det?
Vad menar du med en nettokraft? Menar du kraftresultanten? Ja de finns inga andra krafter på protonen än den elektriska kraften (möjligtvis en tyngdkraft, men räknar du lite på den så ser du att den är oerhört mycket mindre än den elektriska kraften, och kan försummas)
Initialhastigheten v är riktad horisontellt i figuren, alltså är v0y=0, eller hur?
Ja jag menar kraftresultanten, var lite otydlig. Den elektriska kraften agerar då som en resulterande kraft som orsakar en acceleration. Är det korrekt?
Just det. Protonen har ju bara en hastighet i x-led från början. Därav blir formeln för läget/sträckan i y-led:
sy = -gt²/2
Ska man räkna med minustecknet i detta fall eller blir det fel?
Ja jag menar kraftresultanten, var lite otydlig. Den elektriska kraften agerar då som en resulterande kraft som orsakar en acceleration. Är det korrekt?
Ja, det är korrekt.
Just det. Protonen har ju bara en hastighet i x-led från början.
Precis!
Det som avgör om du ska ha med minustecknet eller ej beror på hur du väljer att lägga ditt koordinatsystem. Om du säger att accelerationen är riktad i negativ y-axel-riktning så kommer även den tillryggalagda sträckan att bli negativ, eller hur? Om du hellre vill att protonen ska tillryggalägga en positiv sträcka så låter du y-axeln peka nedåt. Då pekar accelerationen också i den riktningen och är således positiv.
JohanF skrev:Ja jag menar kraftresultanten, var lite otydlig. Den elektriska kraften agerar då som en resulterande kraft som orsakar en acceleration. Är det korrekt?
Ja, det är korrekt.
Just det. Protonen har ju bara en hastighet i x-led från början.
Precis!
Det som avgör om du ska ha med minustecknet eller ej beror på hur du väljer att lägga ditt koordinatsystem. Om du säger att accelerationen är riktad i negativ y-axel-riktning så kommer även den tillryggalagda sträckan att bli negativ, eller hur? Om du hellre vill att protonen ska tillryggalägga en positiv sträcka så låter du y-axeln peka nedåt. Då pekar accelerationen också i den riktningen och är således positiv.
Okej, då hänger jag med. Jag tror det blir smidigare om jag har positiv riktning på sträckan och accelerationen.
Men först tiden t = sx/vx = 0,11/(2,5 * 10⁶) = 4,4*10^-8 s
sy = at²/2 eller ska det vara ett g för a? Kanske prydligare med a?
sy = 2,2 * 10^13 * (4,4*10^-18)²/2 ≈ 0,02 m = 2 cm
Detta betyder väl att protonen böjer av 2 cm neråt. Eller hur ska man förklara det på ett bra sätt?
Bör man inte beräkna någon vinkel också och beskriva att protonen rör sig utefter en parabolisk bana?
Ja, bokstaven g använder man till gravitationsaccelerationen, så använd bokstaven a.
I uppgiften står att du ska beskriva läget i förhållande till där den kom in, så du behöver bara rita in i en figur var den kommer ut någonstans, och var sträckan 2 centimeter är. Din förklaring tycker jag är jättebra, utan vinkel.
Så jag bör rita i figuren att den är någonstans mellan fältlinje två och tre från vänster? Det motsvarar ungefär 2 cm. Blir det fel om man tar med vinkeln i förhållande till horisontalplantet (minus plattan)?
Hur ska man tänka på b uppgiften, där det istället är fråga om en elektron? Frågan är ju hur resultatet skulle förändras då. Krävs beräkningar för detta eller endast ett resonemang? Jag tänker att det borde behövas beräkningar, eftersom massan på elektronen är annorlunda och dess laddning, i jämförelse med en proton. Men jag kanske tänker fel.
såhär skulle jag rita (jag tror du blandade ihop x- och y-led):
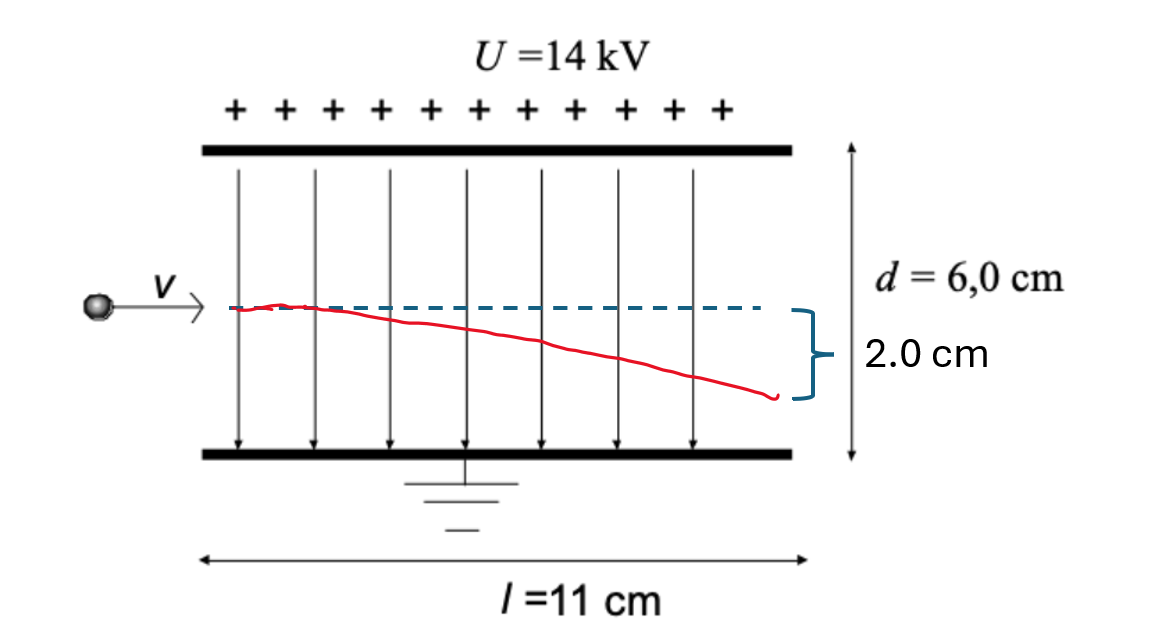
Du klarar dig med endast resonemang på b. Vad är skillnaden på en elektron och en proton (om man bortser ifrån massan, då du ändå inte har använt protonens massa i a)?
Ett par skrivfel efter vägen:
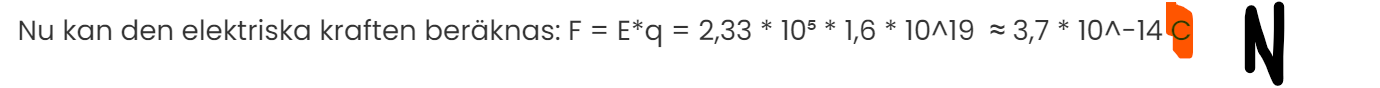
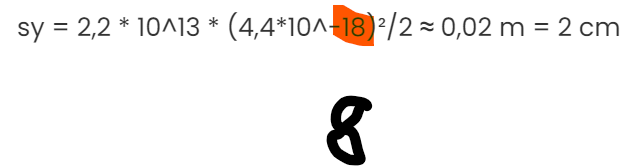
JohanF skrev:såhär skulle jag rita (jag tror du blandade ihop x- och y-led):
Du klarar dig med endast resonemang på b. Vad är skillnaden på en elektron och en proton (om man bortser ifrån massan, då du ändå inte har använt protonens massa i a)?
Ja, jag blandade ihop x-led och y-led, därför blev det fel.
Skillnaden är laddningen. Elektronen kommer istället röra sig mot plusplattan istället. Innebär det att den hamnar 2 cm från plusplattan i vertikal led?
Protonens massa har jag ju däremot använt här:ay = F/m = E*q/m = (3,7 * 10^-14)/(1,67 * 10^-27) ≈ 2,2 * 10^13 m/s².
JohanF skrev:
Ett par skrivfel efter vägen:
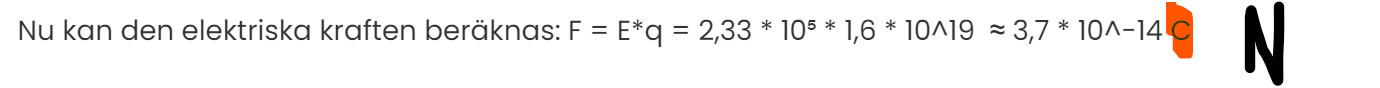
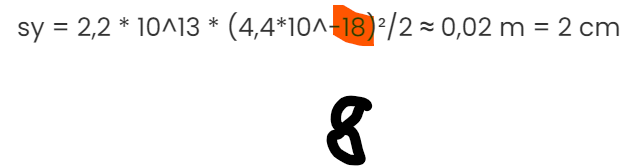
Jag rättar till detta i min lösning. Jag slog dock in 4,4 * 10^⁻8 i miniräknaren så det blev endast ett fel när jag skrev här.. I första raden blir det ju givetvis Newton och inte Coulomb.
violaaa skrev:JohanF skrev:såhär skulle jag rita (jag tror du blandade ihop x- och y-led):
Du klarar dig med endast resonemang på b. Vad är skillnaden på en elektron och en proton (om man bortser ifrån massan, då du ändå inte har använt protonens massa i a)?
Ja, jag blandade ihop x-led och y-led, därför blev det fel.
Skillnaden är laddningen. Elektronen kommer istället röra sig mot plusplattan istället. Innebär det att den hamnar 2 cm från plusplattan i vertikal led?
Protonens massa har jag ju däremot använt här:ay = F/m = E*q/m = (3,7 * 10^-14)/(1,67 * 10^-27) ≈ 2,2 * 10^13 m/s².
Ja just det, du har ju alldeles rätt, du måste beräkna den nya accelerationen med nya massan etc! Det är bra att du ifrågasätter dåliga råd!
Okej då gör jag det :) Återkommer om jag kör fast!
Okej så jag försökte beräkna hur resultatet skulle bli om det istället vore en elektron, men fick väldigt konstiga värden. Här är mina beräkningar:
E = U/d = (14*10³)/0,06 ≈ 2,33 * 10⁵ V/m
F = E*q = 2,33*10⁵ * (-1,6*10^-19) ≈ -3,7 * 10^-14 N. Kraften är negativ eftersom riktningen är negativ uppåt (och positiv nedåt). Stämmer det?
a = F/m = (E*q)/m = -3,7 * 10^-14/9,11*10^-31 ≈ -4,1 * 10^16 m/s². Också här negativt värde pga att riktningen uppåt är negativ (?)
Tiden blir samma som för en proton, dvs. t = sx/vx = 0,11/2,5*10⁶ = 4,4*10^-8 s
Förflyttningen i vertikal led:
s = -4,1*10^16 * (4,4*10^-8)^2/2 ≈ -39,7 m = -3970 cm.
Detta är ett orimligt högt värde. Sträckan i x-led är ju endast 0,11 m och avståndet mellan plattorna 0,06 m. Innebär det att elektronen inte lyckas komma igenom fältet? Eller har jag räknat fel någonstans?
violaaa skrev:Okej så jag försökte beräkna hur resultatet skulle bli om det istället vore en elektron, men fick väldigt konstiga värden. Här är mina beräkningar:
E = U/d = (14*10³)/0,06 ≈ 2,33 * 10⁵ V/m
F = E*q = 2,33*10⁵ * (-1,6*10^-19) ≈ -3,7 * 10^-14 N. Kraften är negativ eftersom riktningen är negativ uppåt (och positiv nedåt). Stämmer det?
a = F/m = (E*q)/m = -3,7 * 10^-14/9,11*10^-31 ≈ -4,1 * 10^16 m/s². Också här negativt värde pga att riktningen uppåt är negativ (?)
Tiden blir samma som för en proton, dvs. t = sx/vx = 0,11/2,5*10⁶ = 4,4*10^-8 s
Förflyttningen i vertikal led:
s = -4,1*10^16 * (4,4*10^-8)^2/2 ≈ -39,7 m = -3970 cm.
Detta är ett orimligt högt värde. Sträckan i x-led är ju endast 0,11 m och avståndet mellan plattorna 0,06 m. Innebär det att elektronen inte lyckas komma igenom fältet? Eller har jag räknat fel någonstans?
Kraften riktas uppåt för att den övre plattan är positivt laddad, och drar till sig den negativa laddade elektronen.
Bra att du reflekterar över ditt svar. Om du går tillbaka i dina beräkningar så ser du vad som händer. Elektronens massa är flera tusen gånger mindre än protonens, och påverkas mycket mer (får högre acceleration) av den elektriska kraften, och dunsar nästan omedelbart in i den övre plattan.
Bra!
Så minus tecknet för kraften innebär att riktningen är uppåt, som jag skrev i föregående svar. Har jag uppfattat det rätt? Samma sak för accelerationen och sträckan? Riktningen uppåt är negativ, då riktningen nedåt sattes som positiv. Är det inte konstigt att sträckan blev negativ, eller brukar det bli så om ena riktningen är negativ?
Elektronen lyckas alltså komma igenom fältet, men rör sig inte den sträckan, då den hindras av plattan (?)
F = E*q = 2,33*10⁵ * (-1,6*10^-19) ≈ -3,7 * 10^-14 N. Kraften är negativ eftersom riktningen är negativ uppåt (och positiv nedåt). Stämmer det?
Stämmer. Kraften är inte negativ för att laddningen är negativ, utan för att kraften är riktad uppåt mot den positivt laddade plattan, och du har definierat uppåt som negativ i ditt koordinatsystem.
Är det inte konstigt att sträckan blev negativ, eller brukar det bli så om ena riktningen är negativ?
Nä, det är inte alls konstigt egentligen, men kan upplevas konstigt.
Man går inte in på det så mycket i gymnasiefysiken, men sträckan är egentligen en koordinat i ditt koordinatsystem. En negativ koordinat betyder att du befinner dig någonstans på negativa delen av din y-axel. Tänker man på det sättet så tror jag det lite lättare att förstå vad en negativ sträcka är.
Elektronen lyckas alltså komma igenom fältet, men rör sig inte den sträckan, då den hindras av plattan (?)
Nä, elektronen kommer inte att ta sig igenom fältet, dvs den kommer inte att komma ut på andra sidan, som protonen gör. Elektronen kommer kommer att dunsa in i den övre plattan så snart den kommer in i fältet.
Hänger du med?
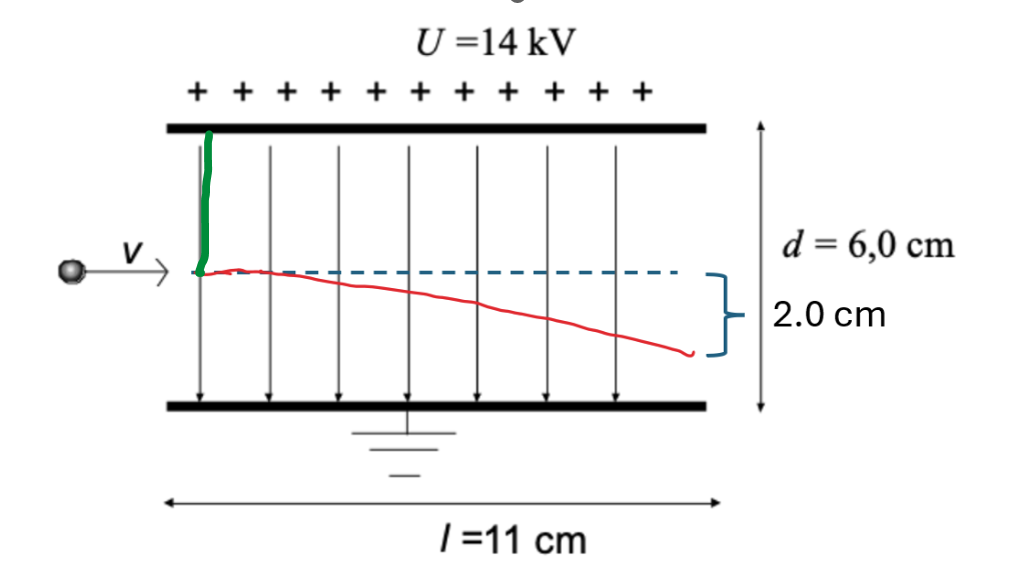
Jag hänger med på nästan allting, behöver endast ett förtydligande på det sista. Den gröna sträckan som du ritat är alltså där elektronen kommer hamna. Men varför har du ritat den just där? Är det pga den höga accelerationen?
Sträckan som den färdas blir således inte 3790 cm, utan den hindras av den positiva plattan pga att den påverkas av den elektriska kraften som orsakar en hög acceleration. Bör man säga hur långt den färdas istället, från startläget tills den når den positiva plattan? Det blir väl 3 cm?
Jag tror inte facit kräver att du gör en exakt beräkning, eftersom man ville att du skulle svara med en position _om_ partikeln kommer igenom fältet. Så jag ritade bara ett streck upp till plattan. Ett kvalitativt svar alltså.
(Att elektronen färdas 3cm i y-led före den slår i plattan behöver du inte svara. Hur långt den färdas i y-led är en följd av det viktiga konstaterandet att den slår i övre plattan)
Men du kan ju om du vill, beräkna hur långt in längs x-led som elektronen hinner (jag blev själv rätt nyfiken på det nu...).
Kan du komma på hur du ska kunna räkna ut det?
Min första tanke var att beräkna hastigheten i y-led men det handlar ju om hur långt elektronen hinner längs x-led, så jag har ingen aning faktiskt. Hur kan man beräkna det?
a-uppgiften gick ut på att beräkna tiden det tog för partikeln att färdas plattans längd i x-led, och sedan därefter räkna hur lång sträcka den hinner färdas i y-led under samma tid. När vi nu vet att partikeln kommer att dundra in i plattan långt innan den har färdats hela plattans längd, så kan det ju vara intressant att se hur långt den egentligen kommer i x-led. Alltså, det kan göras genom att beräkna tiden det tar för partikeln att färdas till plattan i y-led (3cm), och sedan därefter räkna hur lång sträcka den hinner färdas i x-led under samma tid.
Hänger du med?
Jag hänger med på vad vi ska räkna ut, det förstod jag också i ditt föregående meddelande också, men nu hänger jag (nästan) med på hur det ska beräknas.
Okej så tiden i y-led:
t = sy/vy
Hastigheten i y-led (vy) saknas.
vy = ay * t = -4,6*10^16 * 4,4*10^-8 = -2024000000 m/s
t = sy/vy = 0,03/-2024000000 ≈ -1,48 * 10^-11 s
Hur ska man göra nu för att beräkna sträckan i x-led under samma tid? Med denna formel? :
sx = v0x * t + (ax*t^2)/2 Men accelerationen i x-led är ju noll.
sx = v0x * t = 2,5*10^6 * (-1,48*10^-11) ≈ -3,7*10^-5 m = -0,0037 cm (minustecken för riktningen är negativ uppåt)
Är det rätt tänkt?
Nä, inte riktigt. Tiden 44ns som du räknade ut i #7
Men först tiden t = sx/vx = 0,11/(2,5 * 10⁶) = 4,4*10^-8 s
gäller inte alls, eftersom det är den tid det tar _om_ partikeln hade tagit sig igenom fältet till andra sidan, i x-led. Eftersom vi redan vet att detta inte kommer att hända, så kan vi inte använda den tiden, eller hur?
Vi måste istället räkna ut tiden det tar för partikeln att slå in i plattan i y-led. Och rörelsen i y-led beskrivs av formeln du använder i #7
sy = at²/2 eller ska det vara ett g för a? Kanske prydligare med a?
Därifrån kan du få tiden eftersom du känner sträckan 3cm.
Med den nya tiden kan du sedan räkna ut hur långt partikeln hinner i x-led, med sx=vx•t.
Hänger du med? Elektronens rörelse i x-led och y-led beskrivs av precis samma rörelseekvationer som i a. Enda skillnaden i b är att accelerationen är så mycket högre i y-led, att den slår i plattan långt före den skulle ha kommit ut på andra sidan, och därmed blir den intressanta tiden, den av de två tidpunkterna som först inträffar, eftersom den senare tidpunkten aldrig kommer att inträffa.
Oj, ja det är klart att den tiden inte kan användas då. Det är ju tiden som det tar om elektronen tar sig igenom fältet, men den gör ju inte det.
Ur formeln sy = at²/2 ska alltså tiden lösas ut.
t = √(2*sy/a) = √(2*0,03/-4,6*10^16) = -5.32*10^-18 s (kanske borde skippat minustecknet för accelerationen, för tiden blir negativ...)
sx = vx*t = 2,5 * 10^6 * (5,32*10^-18) = 0,133 m = 13.3 cm
Blir det rätt nu? Är lite osäker på om det blev rätt beräknat på miniräknaren gällande tiden.
Jag hänger med på själva situationen nu. Det blir en annan situation i b) uppgiften eftersom elektronen har en lägre massa och därmed en större acceleration i y-led som gör att den inte kommer igenom fältet och slår in i +plattan. Man kan räkna ut hur långt den hinner längs x-led innan den slår in i plattan, vilket är det vi gjort nu.
t=(2*sy/a) = √(2*0,03/-4,6*10^16) = -5.32*10^-18 s
Tiden kan inte vara negativ, accelerationen är negativ och sträckan är negativ. Du slog nog också fel på miniräknaren tror jag.
Jag får tiden t=1.1ns, och därmed sx=2.9mm
Testa att slå det så att för att se om vi får samma.
Det värde jag fick var ju inte rimligt alls, själva längden på plattan är ju endast 11 cm. Jag var för trött när jag löste uppgiften sist.
Tiden kan ju givetvis inte vara negativ, det vet jag.
Tar jag alla värden som positiva så får jag 1,2 ns, så en liten skillnad i jämförelse med ditt värde.
Sträckan i x-led = 2,5*10^6 * 1,2*10^-9 = 0,003 m = 3 mm. Också en minimal skillnad pga skillnaden i tid.
Vi tar dina värden, jag använde avrundade värden.
Du ser att en kvalitativ beskrivning av vad som händer med elektronen är ett streck i figuren, rakt upp i plattan så snart elektionen kommit in i fältet. Eller hur?
Yes! Jag hänger med på det :) Finns det något mer jag bör tänka på eller tycker du detta blir en fullständig och korrekt lösning?
Jag tycker det blir jättebra.
- Försök hitta sammanhangen som gör att den givna informationen (i huvudsak) "makes sense" för det man ska räkna ut. Fundera lite innan du börjar räkna, vad som ungefär borde hända. Då är det lättare att bedöma om det svar man kommer fram till är rimligt eller inte.
- Koordinatsystem. Håll noga koll på vad som gäller i x-led respektive y-led. Positivt eller negativt.
- Slå gärna på miniräknaren ett par gånger. Iallafall jag brukar jämt slå fel nånstans påvägen.
- Svara tydligt, med figur om det behövs.
Vad bra! Tack så mycket för tipsen och för all din hjälp med uppgiften. Uppskattas väldigt mycket! :)