Projecering i ett plan

Hej! Jag försökte lösa denna uppgift men det är några saker jag inte förstår i facit från uppgift a) och b)

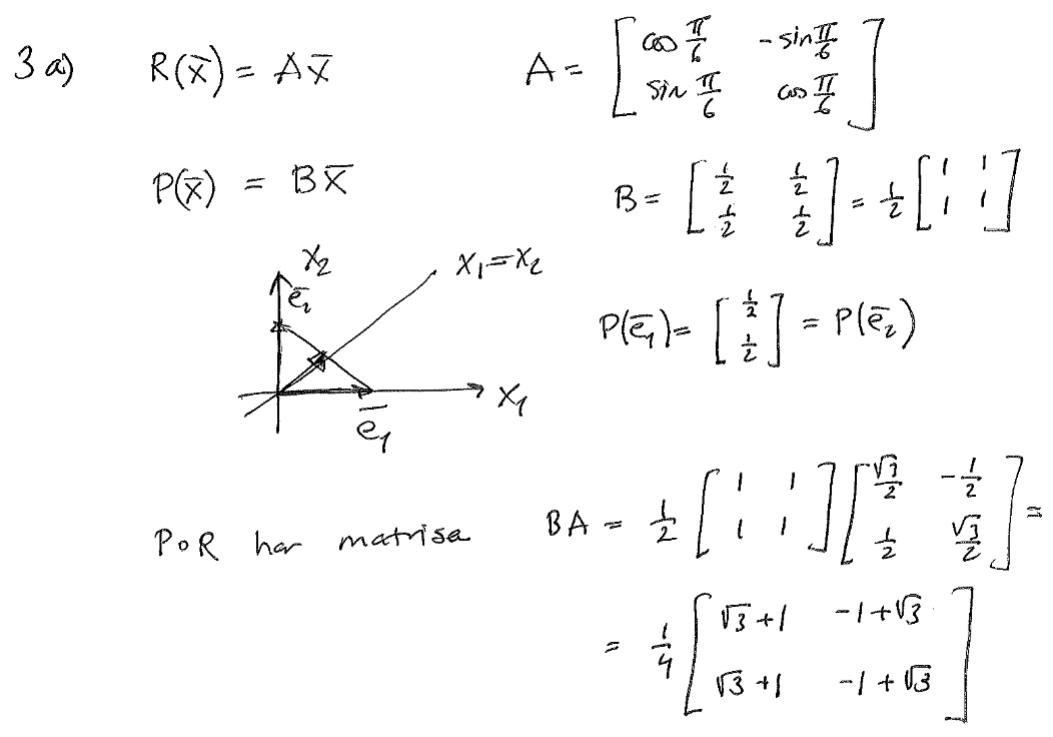
a) Hur kommer man fram till att p(e1) = $[\begin{matrix} 1 / 2 \\ 1 / 2 \end{matrix}]$ ?

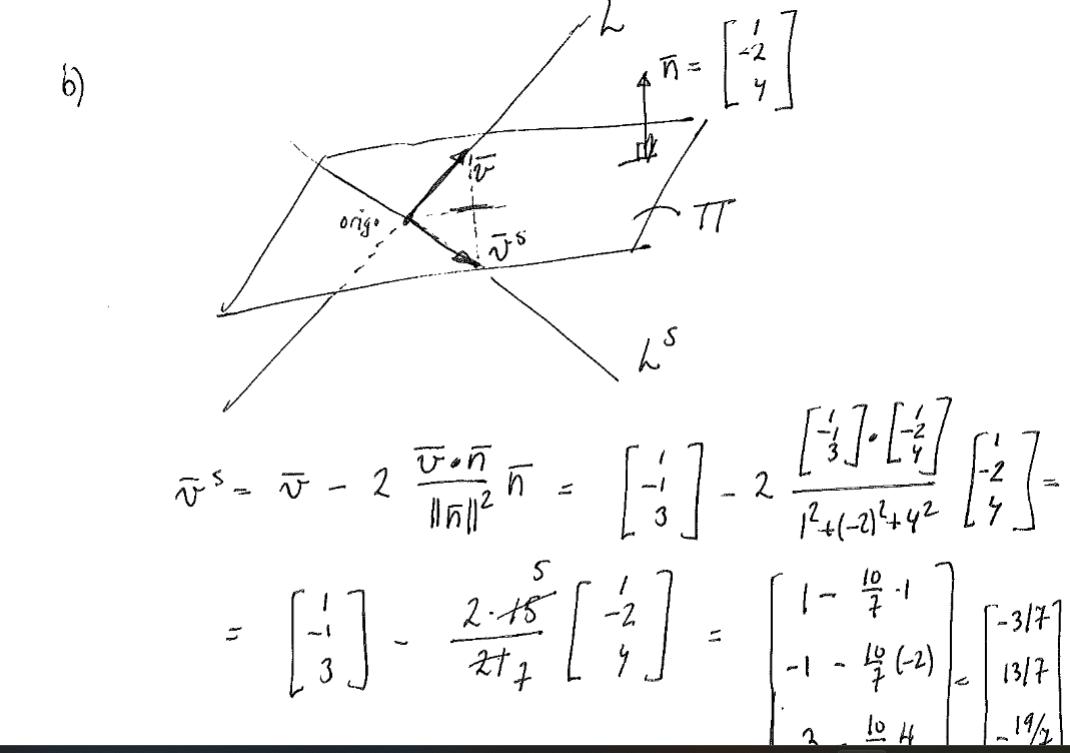
b)Hur kommer de fram till att V^s blir $v - (2 | v * n | n) / | | n | |^{2}$ ? När man gör parameterframställning i en linje brukar det bli att man tar 2p(x) - x och de n härledningen förstår jag men när man ska göra det i ett plan vet jag inte hur man ska tänka? och jag förstår inte varför man använder normalvektorn?

Tack på förhand!

P(e₁) skall ligga på linjen x2 = x1. Så P(e₁) = (a, a) för något a. Från figuren ser vi att a skall vara positivt och att (pytagoras) |P(e₁)| = 1/ $\sqrt{2}$ . |P(e₁)|² = a² + a² = 1/2, vilket ger a = 1/2.

Tack för svar! Jag är med på pytagoras sats delen förutsatt att p(e1) = 1/ $\sqrt{2}$

Jag förstår dock inte varför det p(e1) = 1/ $\sqrt{2}$ ?

Titta på den rätvinkliga triangeln nedan. Hypotenusan har längden 1 och kateterna har längden |P(e₁)|. Pytagoras säger då att |P(e₁)|² + |P(e₁)|² = 1, vilket ger att |P(e₁)| = 1/ $\sqrt{2}$ .

Men varför blir den andra kateten också p(e1)? jag är med på att p(e1) = p(e2) men borde inte det vara en och samma katet? (projecceras de inte till samma katet?) hur vet man att den andra kateten blir samma?

Triangeln är likbent eftersom de icke-räta vinklarna är lika (45˚). Vi ser att det ena benet har längden |P(e₁)| och då är det andra benet lika långt eftersom det är en likbent triangel.

Ah okej förstår jag tack!:) Gör en liknande uppgift idag men då blir dock matrisen basvektorerna istället, känns som nästan samma uppgift, varför blir det annorlunda i detta fall?

I den första uppgiften ortogonalprojicerar du på linjen och i den andra uppgiften speglar man i linjen i stället. En helt annan geometrisk operation, så inte så konstigt om man får en annan matris.

Ah tack nu blev det tydligt, hade tänkt fel:) tack för hjälpen!

Svara

Visa senaste svar