Problemlösning med derivata 2

Vad är det du inte förstår?

Jag förstår inte hur jag ska gå tillväga

Du vet säkert att du ska hitta ett uttryck för arean som beror på x, A(x), där x är någon sträcka i figuren.
Sen kan man på det vanliga sättet derivera och sätta lika med 0, dvs A'(x)=0.

Sambanden är ofta enklare att hitta om trianglarna har räta vinklar. Eftersom hela triangeln och den som ska maximeras är spegelvända i den vertikala mittlinjen, prova att dela triangeln med ett vertikalt streck i mitten.

Rita ny figur.

Två av sidorna på den stora triangeln vet du, kan du beräkna den tredje sidan?

Efter det kanske du kan hitta samband så du kan teckna ett uttryck för arean (eftersom vi delade på mitten kommer uttrycket att vara för halva arean men den kan man ju dubblera på slutet när talet är löst).

Så här

Jag menade efter att du delat den i två så du bara har högra halvan kvar. Dela med höjden i mitten av stora triangeln.

(Man kan göra på flera sätt, det här är bara min första tanke.)

Precis!

Du kan också rita högra halvan ensam så det blir en enklare figur.

Kan du räkna ut 3:e sidan i stora triangeln?

Hmm, alla sidorna är nämnda. 10,10 och 12 cm.

Nu när jag funderar så tänker jag så här.

1. Sätta ett utryck som ger arean för lilla triangeln. Alltså arean på stora triangeln minus arean på de tre trianglarna runt den inritade triangeln.

2. Nu har jag arean på den inritade triangeln.  Så då tar jag (hxb)/2 = arean på den lilla triangeln.

3. Sedan deriverar jag.

Kan detta vara en korrekt plan.

Det kan också fungera. Jag tror det blir lite längre (har inte provat den vägen).

Bara så att du är med på hur jag menade med att dela på mitten och vilken 3:e sida jag pratade om:

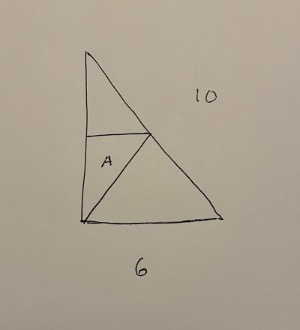
nu förstår jag vad du menar med tredje sidan. Ska börja beräkna det nu. Tack att du ritar

Snyggt (du råkade skriva 18 under triangeln med du menar 6).

Nu gäller det att hitta samband. Tips: med trianglar i trianglar är det ofta likformighet man använder.

Något liknande?

Tillägg: 4 dec 2021 17:42

Jag ser nu att ena sidan är 90 grader, kan man utnyttja det?

Fördelen med 90 grader är att sträckan till vänster om arean är höjden i den triangel du vill skapa ett uttryck för. Kanske ett bra x?

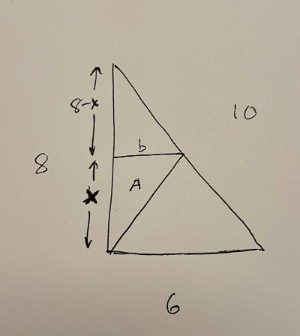
Så jag ska beräkna x på något sätt?

Alltså x bör vara 4 men vet inte hur jag ska bevisa det

(8-×)+×=8

Tillägg: 4 dec 2021 18:01

Känns fel att skriva så

Du behöver ett uttryck gör area som beror av x, A(x), som du sen kan derivera. 

A=xb/2

Du behöver först byta ut b mot något uttryck med x.

Likformighet: ser du att lilla triangeln i toppen har samma form som hela triangeln? Vilket samband kan du få fram mellan sidor i den lilla och den stora triangeln?

Borde det inte vara så här?

Det är nära men ett fel: x är ju inte längden på sidan i lilla triangeln, den sidan är 8-x. Den lilla triangel är ju den i toppen.

Varför blir den X-8. Tittar man på min eller din figur så ser man att sidan för triangel A är x och övre delen 8-×. Men vänder man triangeln så blir det 8-×

Du ska inte ta sidan i triangeln vi söker arean på. Den är inte likformig med den stora triangeln. Det är den i toppen som är det.

Lilla triangeln (i toppen av stora triangeln) har vänster sida 8-x och basen b.

Stora triangeln har vänster sida 8 och basen 6.

Jaha, nu förstår jag. Så man ska ibte titta på den inritade triangeln

Tillägg: 4 dec 2021 18:18

Jag tänkte att jag vände den nedre triangeln så att den blev som den i toppen

Exakt. Ritar man in horisontala linjen långt ner ser man att area-triangeln inte är likformig:

Jag förstår

Nu har du
A=bx/2
och
(8-x)/8 = b/6

Nu kan du teckna A(x)

Hur hittar du sen maxpunkten för A(x)?

Jag börjar fastna lite nu. Så har jag gjort sedan vet jag inte hur jag ska göra.

Tillägg: 4 dec 2021 18:29

Så kanske och sedan sätta in b

Du är nära. Nu kan du ersätta b i uttrycket A=bx/2

Så A(0)=6

Förenkla uttrycket för A(x) först

För att hitta max för A(x) deriverar du A(x) och får A'(x)

Sen sätter du A'(x)=0 och löser ut x

Nu blir det stopp för mig när det kommer till förenkling.

Bra!

Bara så jag vet att ni har fått lära er det:
För att hitta extempunkter för en funktion f(x) är den generella metoden att man deriverar den så man får funktionen f'(x).
Sen sätter man f'(x)=0 och löser ut x.
Sen undersöker man om det (eller de) x man fått ger min- eller maxpunkter.

Nu deriverar du så du får A'(x)

Jo, det har vi fått lära oss. Ska göra det nu, ett ögonblick 

Hur deriverar man nämnaren (16). Ska man flytta upp den till täljsten och sedan sätt upphöjt till minus 1?

Det är rätt. Sätt A'(x)=0 och lös ut x

Så

Det var bra som det var innan (nu blev fel).

Konstanter fram för x är som de är så 16 påverkas inte när du deriverar

Sätt lika med 0 och lös ut x

Blev fel.

16 hamnar i täljaren: 3*16.

Ser du det?

Oj, så ska det va.

Jaha, nu har vi bevisat att x=4

Ja!

De frågar efter längden på sidorna i triangeln som du nu kan beräkna.

(Kom ihåg att vi har arbetat med halva triangeln!)

Och den ska ha så stor area som möjligt, är det därför du tog maximipunkt

Exakt så. Det är så man använder derivatan, för att hitta max eller min.

Eftersom du vet x kan du beräkna b. Och då är det bara hypotenusorna kvar.

Och sen inte glömma att din b är halva basen eftersom vi delade bilden i mitten.

Vad säger du nu?

Ser bra ut!

Svar: Triangeln som har den största möjliga arean har sidlängderna 5, 6, 5

Alltså jag vet inte hur jag ska tacka dig, all den tid du har hjälpt mig. Tusen tack

Det var bara roligt. 

Du ser den generella metoden:
Teckna en funktion f(x) för det man vill hitta max eller min av
Derivera och få f'(x)
Sätt f'(x)=0 och lös ut x
Om du får flera x sätter du in i f(x) för att se vilken som är min och vilken som är max.
(man kan undersöka punkterna med teckenstudium eller andraderivata men vet inte om ni gått igenom det ännu)

Jo, jag ser den nu. Vi har fått lära oss det men det kallades för teckentabell. Det är nog sak samma.

Ja, det är samma som teckenstudium.

Trevlig kväll på dig 😀