Problemlösning, Geometri
Hej!
Jag skulle behöva hjälp med en uppgift. Uppgiften lyder:
I fyrhörningen ABCD är sidorna AB och CD parallella. Linjen l är parallell med AB och CD och delar fyrhörningen ABCD i två till ytan lika stora delar. Visa att:
|PQ| = √|AB|^2+|CD|^22
där P och Q är l:s skärningspunkter med sidorna BC och AD i fyrhörningen.
Hej.
Hur långt har du kommit?
Har du t.ex. försökt att visualisera uppgiften med hjälp av en skiss? Gör annars det.
Hej! Jag har redan gjort skisser. Jag har även skrivit parallellogrammen matematiskt. Men vet ej hur jag ska fortsätta eftersom höjderna är olika (man vet inte). Tänker att h1 och h2 kanske kan göras till hela höjden vid något steg. Har dock inte kunnat komma dit än. Samtidigt skriker PQ = ___ Pythagoras sats. Kommer dock inte på hur allt detta skulle fungera…
Visa gärna dina skisser.
Lösningsförslag
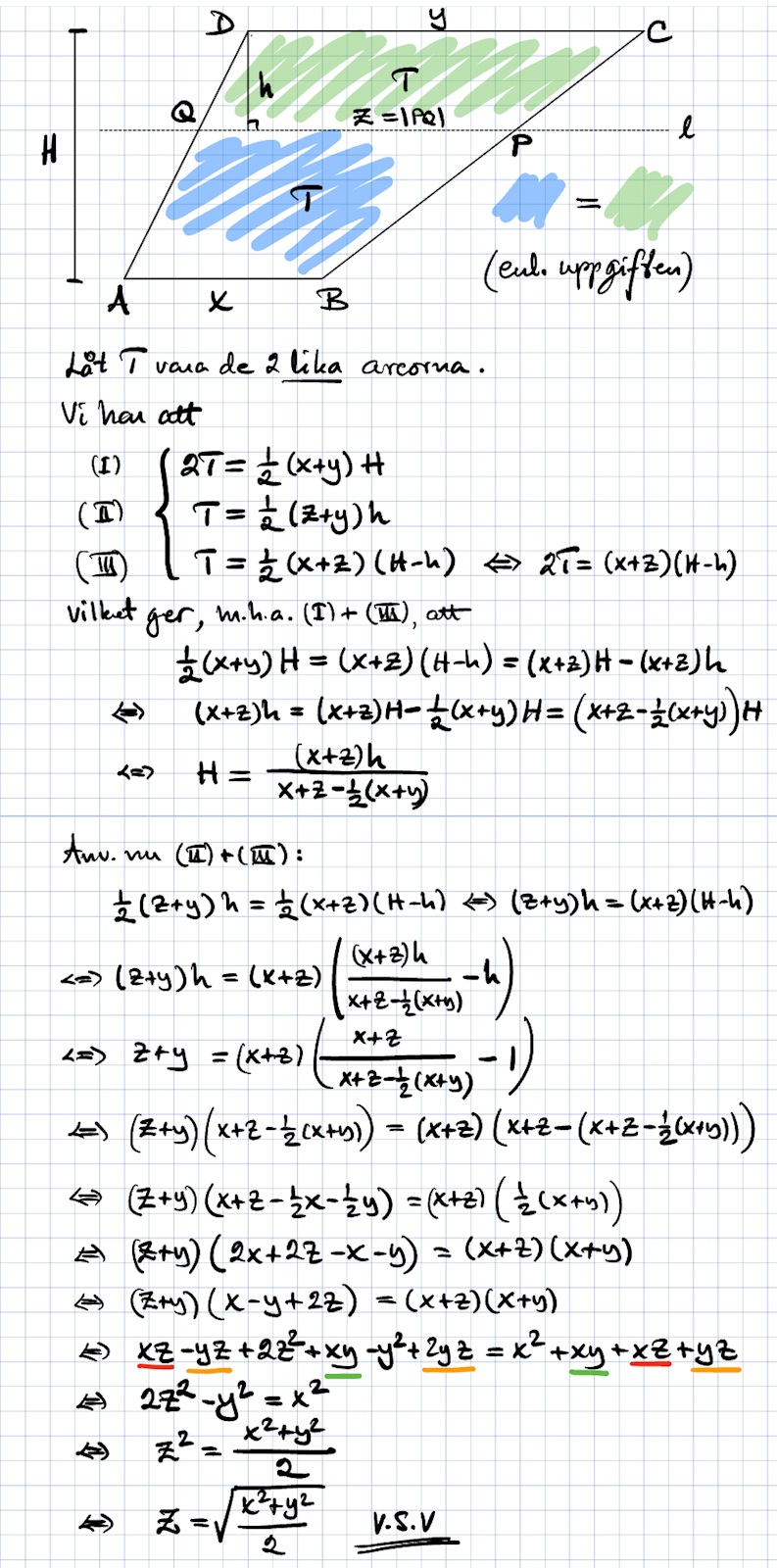
Vi kunde ha inväntat TS:s figur. En variant som ger kortare räkningar är annars att förlänga DA och CB till deras skärningspunkt och använda likformighet. Och att areaskalan är kvadraten på längdskalan. Vi behöver då inte blanda in höjder.
Ställ upp (A + T)/A = (z/x)2, där A är topptriangelns area. Och en ekvation till.
Detta fungerar oavsett form på ABCD, med undantag för om vi har en parallellogram, men då är uppgiftens påstående trivialt.
Nästa gång utelämnar jag skiss och vi får alla nöjet att tolka införda beteckningar fritt efter eget förstånd. Det kan bli ett spännande pussel.
Ska en fullständig lösning presenteras på ett tidigt stadium ingår i denna förstås en figur. Jag tänkte mer på att eftersom Yngve bad TS att visa figuren hen ritat kunde hen få göra det, som utgångspunkt för funderingar över möjliga lösningssätt.
