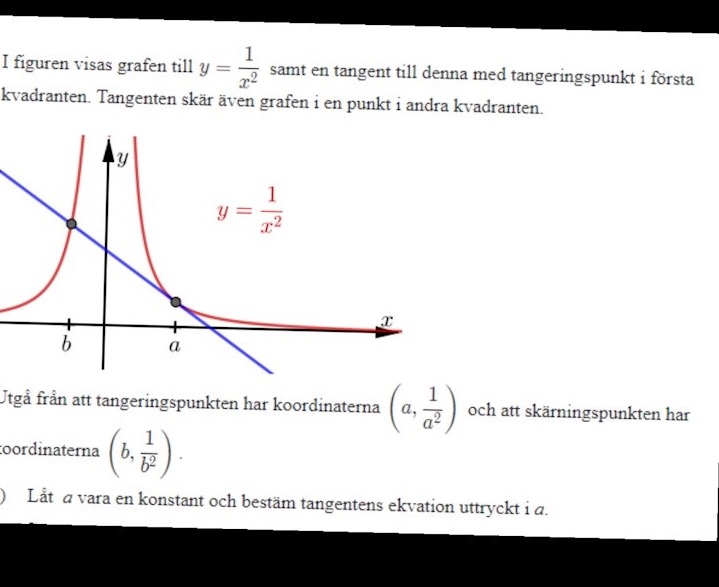
Problemlösning ekvationer
 Jag fick svaret till 3/a^2-2x/a^3=y
Jag fick svaret till 3/a^2-2x/a^3=y
men det finns fråga b som säger att b=-2/a
vet inte hur jag ska lösa den för tänkte att jag bara sätter in b istället för x och 1/b^2 istället för y och gör ekvation av det men det funkar inte
Är det inte b = -a/2?
Louis skrev:Är det inte b = -a/2?
Aha oj råka skriva fel men ja uppgift b vill att man ska visa att b=-a/2
Om du ställer upp ekvationen som du nämner sist är den av tredje graden.
Men den har en dubbelrot, nämligen b=a för tangeringspunkten i första kvadranten.
Så du kan gå vidare och finna den tredje roten (b uttryckt i a).
============
Men du kan också skriva ett uttryck för tangentens lutning med de två punkterna och sätta det uttrycket lika med derivatan i tangeringspunkten.
Louis skrev:Om du ställer upp ekvationen som du nämner sist är den av tredje graden.
Men den har en dubbelrot, nämligen b=a för tangeringspunkten i första kvadranten.
Så du kan gå vidare och finna den tredje roten (b uttryckt i a).============
Men du kan också skriva ett uttryck för tangentens lutning med de två punkterna och sätta det uttrycket lika med derivatan i tangeringspunkten.
 Kommer intevidare
Kommer intevidare
Efter första raden: skriv täljaren i VL på ett bråkstreck, använd konjugatregeln, så kan du förkorta bort a-b.
Du kommer att få en andragradsekvation som med pq-formeln ger två rötter (b uttryckt i a),
där den ena, b=a, kan förkastas.
Louis skrev:Efter första raden: skriv täljaren i VL på ett bråkstreck, använd konjugatregeln, så kan du förkorta bort a-b.
Du kommer att få en andragradsekvation som med pq-formeln ger två rötter (b uttryckt i a),
där den ena, b=a, kan förkastas.
 Så? Jag kommer inte heller vidare
Så? Jag kommer inte heller vidare
Vänstra ledet:
Louis skrev:Vänstra ledet:
Osen? Försökte sätta de lika med varandra gick inte
Satte du det sista uttrycket lika med -2/a3?
Multiplicera båda leden med -a3b2.
Visa ditt försök.

