Problemlösning..

Du behöver inte veta var x = a går, du behöver endast veta hur den går (snett, vågrätt eller lodrätt). Börja med att rita linjen y = 2x + 3. Rita sedan in hur linjen x = a går, var är inte riktigt relevant just nu. 

När du ska räkna ut arean av området, dela upp figuren i några enkla geometriska figurer, och uttryck dessa i termer om a, och sätt detta likamed 28. 

Standardfråga 1a: Har du ritat?

Det står ju i a-uppgiften att det är det du skall börja med.  Linjen $x=a$ är en lodrät linje. Du vet ännu inte var den skall gå, så chansa! Lägg in din bild här, så att vi kan utgå ifrån den.

Smutstvätt skrev:

Du behöver inte veta var x = a går, du behöver endast veta hur den går (snett, vågrätt eller lodrätt). Börja med att rita linjen y = 2x + 3. Rita sedan in hur linjen x = a går, var är inte riktigt relevant just nu. 

När du ska räkna ut arean av området, dela upp figuren i några enkla geometriska figurer, och uttryck dessa i termer om a, och sätt detta likamed 28. 

Kanon nu fick jag fram att x=4 dvs a=4 :)

Men hur får jag fram ekvationen i b) enligt facit så är det enligt följande;

Enligt formeln för ett parallelltrapets:$\frac{\left(\right(2a+3)+3)a}{2}= 28$

Förstår inte :(??

Många tack

Det finns två sätt att beräkna detta på: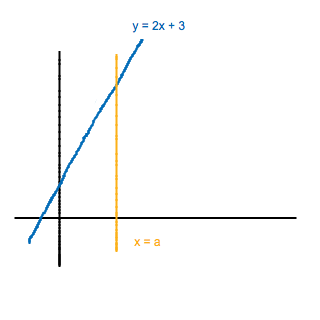Antingen med formeln för arean hos ett parallelltrapets, $A=\frac{h(a+b)}{2}$.  Längden av den lodräta, högra sidan är y(a) = 2a + 3. Längden av den kortare, vänstra sidan är y(0) = 3. Det ger att "a + b" i formeln blir $(2a+3)+3$. Höjden (som i detta fallet är bredden) är a. Ekvationen för arean blir då $A=\frac{a\left(\right(2a+3)+3)}{2}=28$, vilket kan förenklas till $A=a^2+3a=28$.

Det går även att dela upp figuren i två, lite mindre figurer:

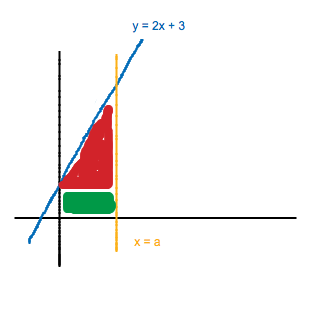
Triangelns area beror på basen a, och höjden, vilken ges som  (y(a) - 3). Dess area blir alltså $A_{\mathrm{triangeln}}=\frac{a\left(\right(2a+3)-3)}{2}=\frac{2a^2}{2}=a^2$. Rektangelns area är $A_{\mathrm{rektangel}}=3a$. Totalt blir arean då $A=a^2+3a=28$. Alltså samma sak. Om man är osäker på formeln för ett parallelltrapets area kan man alltid dela upp den i mindre bitar. 

Smutstvätt skrev:

Det finns två sätt att beräkna detta på:Antingen med formeln för arean hos ett parallelltrapets, $A=\frac{h(a+b)}{2}$.  Längden av den lodräta, högra sidan är y(a) = 2a + 3. Längden av den kortare, vänstra sidan är y(0) = 3. Det ger att "a + b" i formeln blir $(2a+3)+3$. Höjden (som i detta fallet är bredden) är a. Ekvationen för arean blir då $A=\frac{a\left(\right(2a+3)+3)}{2}=28$, vilket kan förenklas till $A=a^2+3a=28$.

Det går även att dela upp figuren i två, lite mindre figurer:

Triangelns area beror på basen a, och höjden, vilken ges som  (y(a) - 3). Dess area blir alltså $A_{\mathrm{triangeln}}=\frac{a\left(\right(2a+3)-3)}{2}=\frac{2a^2}{2}=a^2$. Rektangelns area är $A_{\mathrm{rektangel}}=3a$. Totalt blir arean då $A=a^2+3a=28$. Alltså samma sak. Om man är osäker på formeln för ett parallelltrapets area kan man alltid dela upp den i mindre bitar. 

 Tack snälla du för din hjälp :)

Varsågod!