Problemlösning
I ett rum som är 15 m långt, 6 m brett och 6 m högt sitter en spindel mitt på den ena kortväggen en halv meter från golvet. Mitt på den motsatta väggen sitter en fluga en halv meter från taket. Spindeln vill så fort som möjligt nå fram till flugan. Hur lång är den kortaste vägen mellan spindeln och flugan? Observera att spindeln måste krypa på väggarna.
Min lösning ser ni på bilden. jag vet att mitt svar är fel. Men jag förstår inte vilka fel jag gör. Skulle vara tacksam för hjälp..

Du har räknat i två dimensioner! Då blir det knas. Precis som att gå längs hypotenusan i en rektangel är kortare än att gå längs väggarna, är det kortare att gå i ett rätblocks "hypotenusa" än att gå ned längs väggen längs golvet och upp längs väggen igen. Detta är situationen:
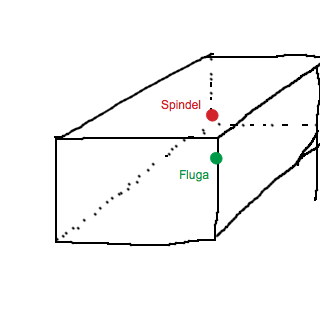
Och den kortaste vägen är denna:
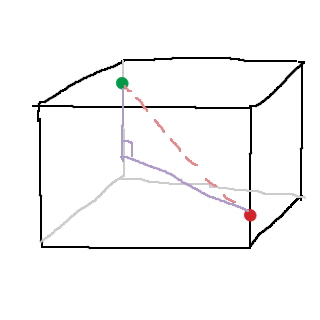
Den horisontella lila linjen har du räknat ut. Hur lång är den vertikala lila linjen?
Edit: Nevermind.
Smutstvätt skrev:Du har räknat i två dimensioner! Då blir det knas. Precis som att gå längs hypotenusan i en rektangel är kortare än att gå längs väggarna, är det kortare att gå i ett rätblocks "hypotenusa" än att gå ned längs väggen längs golvet och upp längs väggen igen. Detta är situationen:
Och den kortaste vägen är denna:
Den horisontella lila linjen har du räknat ut. Hur lång är den vertikala lila linjen?
Det ser ut som om djuren sitter i hörnen i din bild, men de skulle ju sitta mitt på kortväggarna. Eller så ser det bara konstigt ut på min mobil.
Vet inte hur jag ska beräkna vertikal linjen. Det är inte en direkt sida utan flera som måste beräknas?
@Laguna: Attans! Någon här har inte läst tillräckligt noga. Tack! Här är en bättre bild:
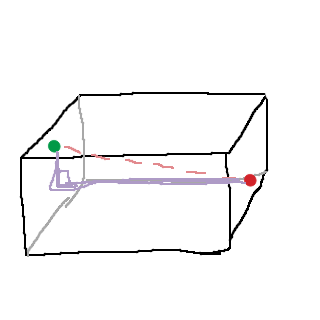
Den horisontella sträckan är lika med väggens långsida. Hur lång är den korta sidan?it:
Edit: Jag är hopplös idag.
Här ser det ut som om spindeln kan flyga, men den skulle krypa på väggarna.
Jag tror det här är en gammal Martin Gardner-uppgift från hans "Rolig matematik" och inte alls uppenbar att lösa med bara Pythagoras sats. Dvs, man behöver inte mer matte än så, men man måste tänka på ett klurigt sätt.
Rita gavelväggen och rita in spindeln. Rita långväggen emellan. Rita sist andra gavelväggen och rita in flugan Dra en rät linje och räkna sedan.
Den här uppgiften är inte enkel, åtminstoneinte om man placerar spindeln och flugan osymmetriskt på väggarna - det går att "veckla ut" rummet på flera olika sätt, och det är inte självklart vilket sätt som ger den kortaste vägen. Jag har ett svagt minne från Gardners bok att vägen passerar över 4 olika sidor,
Antingen
- klättrar spindeln via taket (eller golvet)
Eller
- klättrar spindeln enbart på väggar
Rita de två fallen, och jämför. I det första fallet spelar det ingen roll om spindeln väljer tak eller golv (varför inte?)
Observera att spindeln måste krypa på väggarna.

Tänker jag rätt? Ska jag beräkna längden utav sträcket?
observerar att orange pricken var spindel och gröna flugan!
Undrar dock hur man beräkna sträcket. Vid första kvadraten är hypotenusan 16m + den andra hypotenusan.
Nej, rita bara tre väggar. En korsida, en långsida och en kortsida. Alla tre bredvid varandra. Inget tre -d. Bara rektanglar.
Rita i spindeln på en kortvägg och flugan på andra kortväggen. Den långa väggen i mitten. Dra sedan en rak linje från spindeln till flugan och nu har du en rätvinklig triangel som du kan räkna ut hypotenusan på om du drar några vågräta streck också.
Vad menar du med att bara rita 3 väggar??
 Har ritat om den, tror att jag löste frågan, trots att jag inte förstod resonemanget..
Har ritat om den, tror att jag löste frågan, trots att jag inte förstod resonemanget..
lösningen : 5,5m upp så att spindeln hamnar på taket + hypotenusa av taket som är 16m . 16m+5,5m=21,6m

Så här tänker jag mig spindelns promenad. De andra måtten har du fått med uppgiften.
Varför ritar du 2 kvadrater och en rektangel? Förstår inte? Är min metod/ tankesätt?
Texten stämmer inte med dina figurer.
Spindeln och flugan sitter mitt på kortväggarna, nära golvet respektive taket. Så här:

Nu markerar jag en långsida röd:

...och om vi nu tänker oss rummet som en pappkartong, så klipper jag sönder kartongen och viker upp den. De tre färgade sidorna sitter ihop.

Bara så ni vet: det finns en lösning som är mindre än 21 m.
Kan den här tråden ha något med denna länk att göra?
http://mathworld.wolfram.com/SpiderandFlyProblem.html
I så fall har vi fått fel förutsättningar. Där får spindeln använda både golv och tak enligt denna figur.

Laguna skrev:Bara så ni vet: det finns en lösning som är mindre än 21 m.
Jahaja, det står "på väggarna". Då drar jag tllbaka mitt påpekande.
Nelly1455562 skrev:Varför ritar du 2 kvadrater och en rektangel? Förstår inte? Är min metod/ tankesätt?
Förstår du hur vi menar nu Nelly efter Bubos och mina figurer? Har du rätt svar och vill du ha hjälp att komma fram till det?
Det står att spindel står 1,5m från marken och att den står i mitten av väggen. Hur går det ihop?
tack till alla som hjälper !
1,5 meter ovanför golvet och lika långt från högerväggen som från vänsterväggen.
I ett rum som är 15 m långt, 6 m brett och 6 m högt sitter en spindel mitt på den ena kortväggen en halv meter från golvet. Mitt på den motsatta väggen sitter en fluga en halv meter från taket.
En halv meter är 50 cm.
Nelly1455562 skrev:Det står att spindel står 1,5m från marken och att den står i mitten av väggen. Hur går det ihop?
tack till alla som hjälper !
"Mitten" måste betyda mitten i sidled, inte i höjdled. Annars går det inte ihop.
Jag håller med om att det är en dålig formulering.
Ok, men fortfarande förstår jag inte hur ett rum med 4 väggar ska ha 3. Jag är lite förvirrad när det kommer till att rita rummet... :/
Smutstvätt skrev:Du har räknat i två dimensioner! Då blir det knas. Precis som att gå längs hypotenusan i en rektangel är kortare än att gå längs väggarna, är det kortare att gå i ett rätblocks "hypotenusa" än att gå ned längs väggen längs golvet och upp längs väggen igen. Detta är situationen:
Och den kortaste vägen är denna:
Den horisontella lila linjen har du räknat ut. Hur lång är den vertikala lila linjen?
Edit: Nevermind.
Kan jag inte rita som den här
Har löst uppgiften, jag hoppas att det är rätt.
Först så tar det 3m för spindel att klättra ner till golvet, för att sedan klättra till andra väggen måste jag beräkna hypotenusa som är ungefär 16m. Vidare får vi reda på att flugan sitter mitt på halv väggen dvs 3m från. (Enligt texten får spindeln inte flyga dvs måste den klättra på väggen)
3+16+3=22m (avrundat)
stämmer resonemanget?
Nej.
Här är en video på ungefär samma problem, med rummet "utvikt". Ser du då vad jag har försökt rita?
(spindeln och flugan är lite annorlunda placerade, och spindeln får gå i tak och golv också)
https://www.youtube.com/watch?v=KlDwT2l1K6k
ConnyN skrev:Kan den här tråden ha något med denna länk att göra?
http://mathworld.wolfram.com/SpiderandFlyProblem.html
I så fall har vi fått fel förutsättningar. Där får spindeln använda både golv och tak enligt denna figur.
Det borde ju vara 4 sidor, varför är det 6 sidor på bilden??
 Om jag följer den här ritningen vart är taket isåfall? Jag har förstått att den långa sidan är golvet och att de korta sidorna är väggarna, men taket?
Om jag följer den här ritningen vart är taket isåfall? Jag har förstått att den långa sidan är golvet och att de korta sidorna är väggarna, men taket?
Där har man "klippt upp och vikt ut" alla sidor i lådan: kortväggar, långväggar, golv och tak.
I flera andra figurer här har man struntat i de sidor som inte är intressanta för just den figuren.
Så det innebär att taket inte ska finnas med???
Isåfall blir uträkningen på följande sätt :
3+15+3=21m
Bubo skrev:Nu markerar jag en långsida röd:
Kan man inte lösa uppgiften genom att använda sig av den här bilden ovanför??
Nelly1455562 skrev: Kan man inte lösa uppgiften genom att använda sig av den här bilden ovanför??Bubo skrev:
Kan man inte lösa uppgiften genom att använda sig av den här bilden ovanför??
Ja det är bara det att spindeln sitter 0,5 meter från golvet och att flugan sitter 0,5 meter från taket.
Du skrev tidigare att
"Först så tar det 3m för spindel att klättra ner till golvet, för att sedan klättra till andra väggen måste jag beräkna hypotenusa som är ungefär 16m. Vidare får vi reda på att flugan sitter mitt på halv väggen dvs 3m från. (Enligt texten får spindeln inte flyga dvs måste den klättra på väggen)
3+16+3=22m (avrundat) stämmer resonemanget?"
Där börjar du att tänka rätt. Du använder tre väggar, precis som jag försökte beskriva.
Om du tittar på Bubos figur och "vecklar ut de tre väggarna, så ser du att du kan dra en rät linje mellan punkterna och det visar spindelns promenad snett upp på kortväggen, den fortsätter snett upp över hela långväggen och avslutas snett upp på kortväggen och förhoppningsvis sitter flugan kvar?
Jaha men då förstår jag felet! Felet låg alltså på placeringen av spindeln och flugan. Spindel ska vara 0,5m från marken men på mitten av halvväggen. Flugan ska vara 0,5m från taket. Så felet var alltså på placeringen men själva resonemanget var rätt??
Bra nu börjar vi närma oss.
Du ritar alltså en kortvägg och som du skriver " Spindel ska vara 0,5m från marken men på mitten av halvväggen." Helt rätt.
Sedan ritar du långväggen som än så länge är tom.
Därefter ritar du nästa kortvägg med flugan på och som du skriver "Flugan ska vara 0,5m från taket". Helt rätt.
OBS rita de tre väggarna bredvid varandra.
Nu kan du prova ditt resonemang och föreställa dig promenaden på de tre väggarna.
 Lösning : 3m+ hypotenusa+3.
Lösning : 3m+ hypotenusa+3.
3m från spindelsvägg till väggen i mitten, vidare räknar jag längden på väggen i mitten genom Pythagoras sats sedan subtraherar jag 1m för att det inte exakt vid kanelen som linjen sträcker sig. Dvs hypotenusa : 16-1=15m
3+15+3=21m
stämmer det?
Snygg ritning!
Däremot är din lösning inte riktig.
Om du tänker att du drar en linje rakt ner från flugans position och slutar 0,5 m från golvet, så har du höjden på triangeln.
Den blir 6 - (0,5 + 0,5) = 5 meter.
Basen är den vågräta linjen från spindelns startpunkt till 3 meter in på högra kortväggen och den sträckan blir däremot 3+15+3 = 21 m.
Nu kan du räkna ut hypotenusan med pythagoras sats och där har du hela sträckan.
Vi vet att a : 6-1=5m
b : 3+15+3=21m
C får vi fram genom att använda oss av pythagoras sats på följande sätt 5^2+21^2=c^2
C är ungefär 21,6m.
Stämmer det?
 Här är en bild på hur det ska se ut, ber om ursäkt för otydlig bild.
Här är en bild på hur det ska se ut, ber om ursäkt för otydlig bild.
Hej!
Det ser ju jättebra ut (inte bilden kanske den här gången)
men uppställingen och uträkningen ser ut som en dröm :-)
 Här är en bättre bild :) är svaret/lösningen korrekt?
Här är en bättre bild :) är svaret/lösningen korrekt?
Ja det är rätt och bilden är fin.





