Primtiv funktion och derivata
Hej, har stött på denna uppgift:
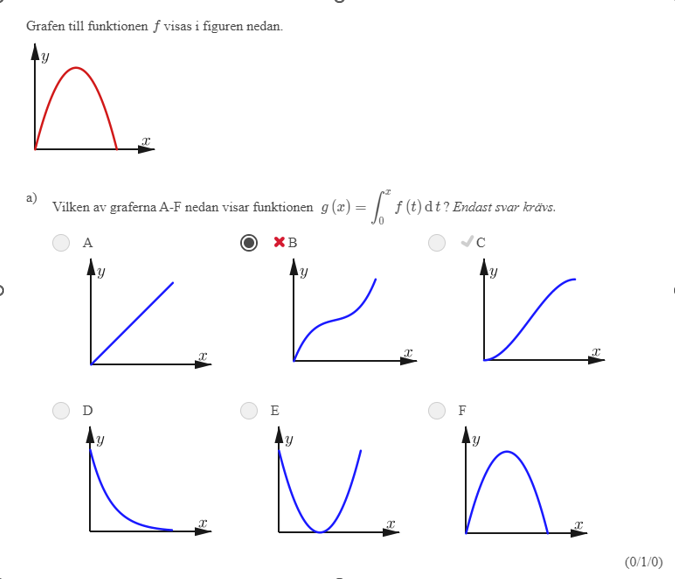
Jag förstår inte varför mitt svar är fel. Jag tänker följande:
Om g(x) = gäller att g(x) = F(x) - F(0) där F(0) = 0. Alltså beskriver g(x) den primitiva funktionen till f(x) då t = x. f(x) är ju en andragradsfunktion och då blir den primitiva funktionen en tredjegradsfunktion. Alltså står det mellan B och C. Jag är lite osäker på vilken av dessa som representerar en parabel med negativ x^2 koefficient, men jag chansade på B. Tänker jag rätt? Går det att säga med säkerhet om det är B eller C? Fungerar mitt resonemang?
Kanske är det ännu enklare att tänka "sträcka och hastighet".
Hastighet är ju tidsderivatan av sträckan, så sträckan är primitiv funktion till hastighet.
Om hastigheten v(t) hos en bil ser ut som den röda kurvan, hur ser då sträckan s(t) ut?
Röda kurvan:
Bilen kör inte fort i början och slutet (vid tiden noll och vid stort värde på tiden) men rejält fort mitt i tiden.
Eller så tänker du tvärtom - hur ser grafen för derivatan g'(x) ut?
Tack för svar! Så min metod fungerar ej?
Eftersom vi bara ser en del av kurvan vet vi inte om den går mot plus oändligheten eller minus oändligheten för stora x.
Den negativa koefficienten för x^2 ger oss att den borde gå mot minus oändligheten, men det är inte så lätt att avgöra om B eller C tänker göra det för riktigt stora x.

