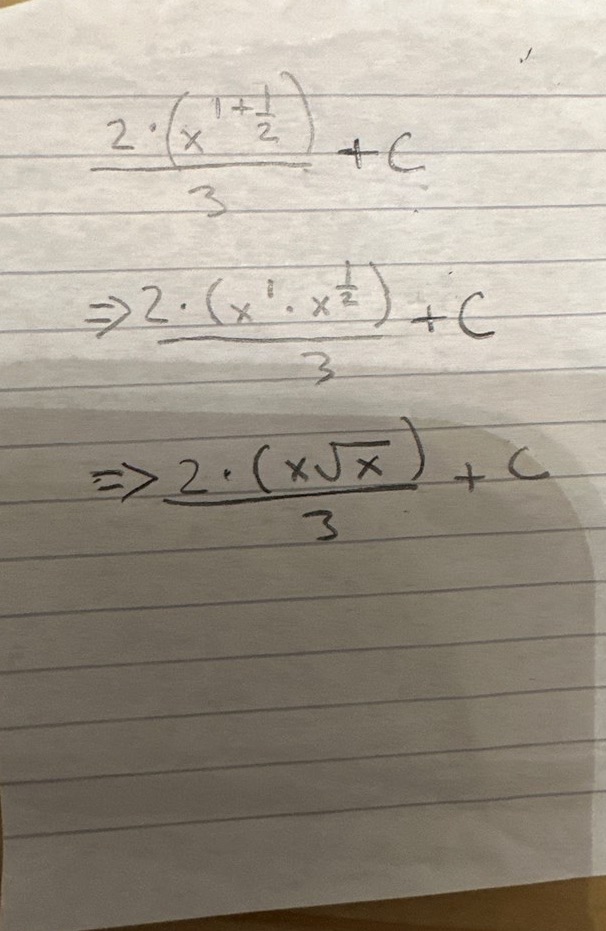Primitiva funktioner

a), b)

Tänk på att du alltid kan testa om din primitiva funktion är rätt. (Och glöm inte integrationskonstanten!) Derivera det du har fått fram. Vad får du? 

c)

n = 1/2. Du kan använda formeln du har skrivit uppe till höger. 

Då har du fått rätt primitiva funktioner!

Ibland glömmer du integrationskonstanten. Förenkla bråken, t.ex 2/2. 

Skilj på stora och små bokstäver. 

Om G(x) är primitiv funktion till g(x) så är G'(x) = g(x).

Ok, och är integrationskonstanten ……+C 

?

Ja, den skrivs vanligen C. 

Såhär?

är det de samtliga primitiva funktioner?

Bra!

De primitiva funktionerna ör rätt.

Antagligen bör man skriva $x\sqrt{x}$ istället för $x^{\frac{3}{2}}$ på sista.

Men jag blir fundersam när du skriver enligt de gulmarkerade delarna. Betyder det "primitiva funktionerna till", dvs att t.ex. (x²+3) betyder "primitiva funktionerna till x²+3"?

Om ja så är det något jag aldrig sett tidigare och väldigt vilseledande.

Om nej så är det bara felaktigt skrivet.

Nej, du har rätt

De gulmarkerade ska tas bort

Hur menar du att x^3/2 kan skrivas till x√x  ?

går det bra att göra det mot slutet?

pga potenslag?

Biorr skrev:

Hur menar du att x^3/2 kan skrivas till x√x  ?

$x^{\frac{3}{2}}=x^{1+\frac{1}{2}}=x^1\cdot x^{\frac{1}{2}}=x\cdot\sqrt{x}$

går det bra att göra det mot slutet?

Ja

pga potenslag?

Ja, det är $x^a\cdot x^b=x^{a+b}$

Ja, det stämmer.

En detalj, du bör skriva = istället för $\Rightarrow$ eftersom uttrycken är ekvivalenta.