Primitiv funktion för tanx

Derivatan av cos(x) är -sin(x), vad kan då vara en lämplig sub?

Hänger inte med, jag vet i alla fall att man kan substituera den inre funktionen till t. Men jag har ingen inre funktion? Eller är cos x=t och dt=1 dx?

Du har det på form:

$- \displaystyle \int \dfrac{f^\prime (x)}{f(x)}$ eftersom $D(\sin x )= - \cos x$

Denna integralen vet du nog hur man integrerar, eller hur?

Nja, inte riktigt. Räknar man ut täljaren och nämnaren separat?

Vad är derivatan av $\ln (f(x))$?

1/$\left|f\left(x\right)\right|$

Nej, samma sak som vi pratade om i din förra tråd. Du har en komposit:

$g(x) = \ln (x)$ så att $h(x)=g(f(x))$

Applicera kedjeregeln.

Det blir ju g(ln|x|)

Här nedan försökte jag hitta den inre och yttre funktionen men gick inte så bra.

Ja, det går ju också att göra så om man vill.

Men du har vänt på det.

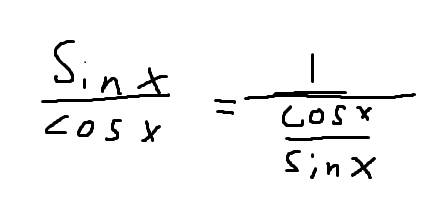
Varför blev det fel när jag bytte plats på de två?

Jag förstår inte riktigt varför du skulle vilja vända på det? Då har du en helt annan funktion. 

Det blir ju g(ln|x|)

Om detta är svaret till inlägg #8 så är det fel. 

Angående inre och yttre funktion så kan man säga att f(x)=1/x, så jag valde att ersätta x med sin (x)/cos(x) dvs $\frac{1}{{\displaystyle \frac{\sin \left(x\right)}{Cos \left(x\right)}}}$

Men då får du inversen till din funktion. Varför vill du ha det? 

Om du gör som jag gjort ovan (som jag antog du menade?) så kan du använda en sub som formeln du hänvisar till ovan gör för då är det på exakt samma form. Men allt detta är onödigt.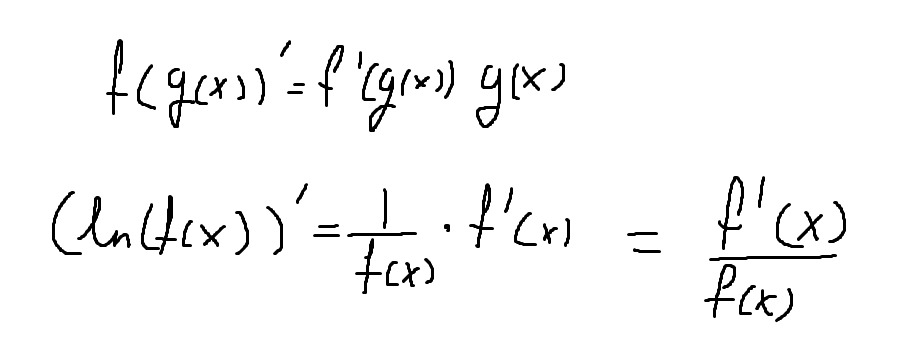 

Det var lite detta jag ville du skulle komma fram till genom att lösa derivatan jag frågade efter i inlägg #4 och #8

Tillägg: 15 dec 2022 20:54

Notera att det ska vara $f^\prime (g(x)) g^\prime (x)$ på bilden egentligen.