primitiv funktion

Har du ritat? Såhär ser grafen ut. Det område vars area ska beräknas är det ovalformade objektet i mitten. Dess area kan beräknas genom att hitta arean för det område som begränsas av $y=16-x^{2}$ och x-axeln, och ligger mellan skärningspunkterna (orange):

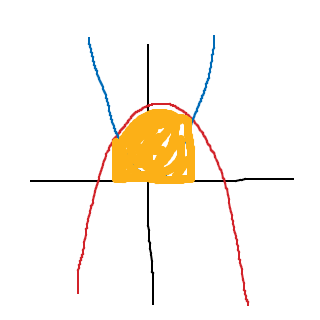
Och därefter subtrahera arean som är utanför (ljusblått):

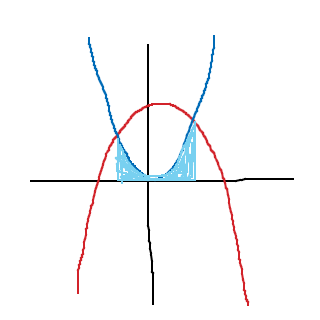
För att ställa upp dessa integraluttryck måste du först hitta skärningspunkterna mellan funktionerna. Du har börjat med det, men ej gjort klart din uträkning. Lös för vilka två x-värden som ger att $y_{1}=y_{2}$. Dessa sätter du sedan som integralgränser när du ställer upp dina integraler.

basinski: Vill du ha enklare räkningar utnyttjar du symmetrin i grafen.

$\displaystyle\int_{-2}^2 \cdots \,\mathrm{d}x=2\int_0^2 \cdots \,\mathrm{d}x=\cdots$

Och, vad är $16-x^2-3x^2$?

Trinity skrev:

basinski: Vill du ha enklare räkningar utnyttjar du symmetrin i grafen.

$\displaystyle\int_{-2}^2 \cdots \,\mathrm{d}x=2\int_0^2 \cdots \,\mathrm{d}x=\cdots$

Och, vad är $16-x^2-3x^2$?

 det är väl ekvationen utifrån ekvationssystemet, hur ska man göra annars?

basinski skrev:

det här blir fel, hur bestämmer man den primitiva funktionen?

Du har tänkt rätt och räknat rätt fram till sista uträkningen, där du helt enkelt har glömt parenteser, vilket gör att du får fel tecken på en del termer.

Sista steget ska vara

$(16\cdot 2-\frac{2^3}{3}-\frac{3\cdot 2^3}{3})-(16\cdot (-2)-\frac{(-2)^3}{3}-\frac{3\cdot (-2)^3}{3})$

Räkna vidare därifrån.

Sen går det ju som sagt att förenkla en del innan integralen beräknas.