pq formel tredje grad

Om man löser ut x som du gjort i ditt första steg kan man se att hela uttrycket blir noll om antingen x=0  eller parentesen är lika med 0. Så en av lösningarna är x=0. De andra två lösningarna får du genom att hitta alla nollställen till andragradsekvationen inne i parentesen.

Dock har du fel tecken framför 5 när du använder pq-formeln.

Svaren blir x=0,  x=4-sqrt(11)  x=4+sqrt(11)

Svaren blir x=0,  x=4-sqrt(11)  x=4+sqrt(11)

Så svaret jag skrev på x1 och x2 är egentligen x1=4-sqrt(11) x2=4+sqrt(11)

Men hur fick du att x3 = 0? Och hur vet man vilken av dem som inte är realla och inte? ''inte helt säker vad realla på ekvationer som dessa betyder däremot''

Varför struntar vi i x innan parantesen när vi räknar med PQ formel? hur använder vi den för att räkna värdet på x möjlighet 3?

Alla polynom av grad n kan skrivas på formen k(x-x₁)(x-x₂)...(x-x_n), där x₁, x₂... x_n är polynomets nollställen och k är konstanten framför x-termen av högst grad. Alla polynom kan alltså skrivas som en produkt av ett tal k och dess nollställen.

När vi använer pq-formeln så letar vi efter andragradspolynomets nollställen för att kunna faktorisera det på formen ovan (nollställesform).

naytte skrev:

Varför struntar vi i x innan parantesen när vi räknar med PQ formel? hur använder vi den för att räkna värdet på x möjlighet 3?

Alla polynom av grad n kan skrivas på formen k(x-x₁)(x-x₂)...(x-x_n), där x₁, x₂... x_n är polynomets nollställen och k är konstanten framför x-termen av högst grad. Alla polynom kan alltså skrivas som en produkt av ett tal k och dess nollställen.

När vi använer pq-formeln så letar vi efter andragradspolynomets nollställen för att kunna faktorisera det på formen ovan (nollställesform).

Vilken är konstanten? Och hänger inte riktigt med, det ser ut som du skriver andrakvaderings regel och då måste x1 och x2 vara lika värden?

När vi använer pq-formeln så letar vi efter andragradspolynomets nollställen för att kunna faktorisera det på formen ovan (nollställesform).

Tror jag förstår detta däremot, eftersom varje kurva är en andragradspolynom? och vi letar efter nollställen på varje av dem kurvorna (det finns 2 kurvor på en tredjegradsfunktion och 3 på en fjärdegradsfunktion)? Och därmed är x2 och x3 nollställen för hela andra kurvan och symmetri linjen mellan dem då. Men förstår fortfarande inte hur man får värdet på nollstället av x3

Men om det finns 2 kurvor då finns 2 symmetrilinjer?

$x^3-8x^2+5x=0$ kan skrivas som $x(x^2-8x+5)=0$ precis som du gjort.

1. Om x innan perentesen är 0 blir ju yttrycket 0 x (andragadsekvationen). Svaret är 0 och därför är x=0 en lösning.

2. Om andragradsekvationen är noll blir perentesen noll och då kommer hela uttrycket också bli noll. Det finns två x-värden på din ekvation som gör att perentesen blir noll. Det är x=4-sqrt(11) och x=4+sqrt(11). Dvs lösningarna på andragradsekvationen i perentesen.

lagminator skrev:

$x^3-8x^2+5x=0$ kan skrivas som $x(x^2-8x+5)=0$ precis som du gjort.

1. Om x innan perentesen är 0 blir ju yttrycket 0 x (andragadsekvationen). Svaret är 0 och därför är x=0 en lösning.

2. Om andragradsekvationen är noll blir perentesen noll och då kommer hela uttrycket också bli noll. Det finns två x-värden på din ekvation som gör att perentesen blir noll. Det är x=4-sqrt(11) och x=4+sqrt(11). Dvs lösningarna på andragradsekvationen i perentesen.

Förstår tack. Vilka av dem är då realla/inte realla, vad det än betyder?

Förresten vi är nästan säkra på att x = 0 när den är på y led = 5 eller hur, vilket ger första púnkten på nollstället, och sen är det bara att utveckla en värde tabell där x = 1,2,3,4,5,6 intills y-värdet minskar? och om yvärdet minskar så blir det en ny kurva. Om den fortsätter att minska så är det alltså ingen extra grad

Alla de tre lösningarna är reella, annars hade du inte kunnat skriva dem med reella tal, dvs tal som finns på tal-linjen.

Vad menade du med "varje kurva är ett andragradspolynom"?

Laguna skrev:

Vad menade du med "varje kurva är ett andragradspolynom"?

Varje kurvas ändringspunkt

Det där förstod jag inte alls.

Laguna skrev:

Det där förstod jag inte alls.

när en kurva blir till en ny kurva

''Förresten vi är nästan säkra på att x = 0 när den är på y led = 5 eller hur, vilket ger första púnkten på nollstället, och sen är det bara att utveckla en värde tabell där x = 1,2,3,4,5,6 intills y-värdet minskar? och om yvärdet minskar så blir det en ny kurva. Om den fortsätter att minska så är det alltså ingen extra grad'' det jag menar med ändringspunkten

Jag förstår ändå inte. Hur blir en kurva en ny kurva?

Laguna skrev:

Jag förstår ändå inte. Hur blir en kurva en ny kurva?

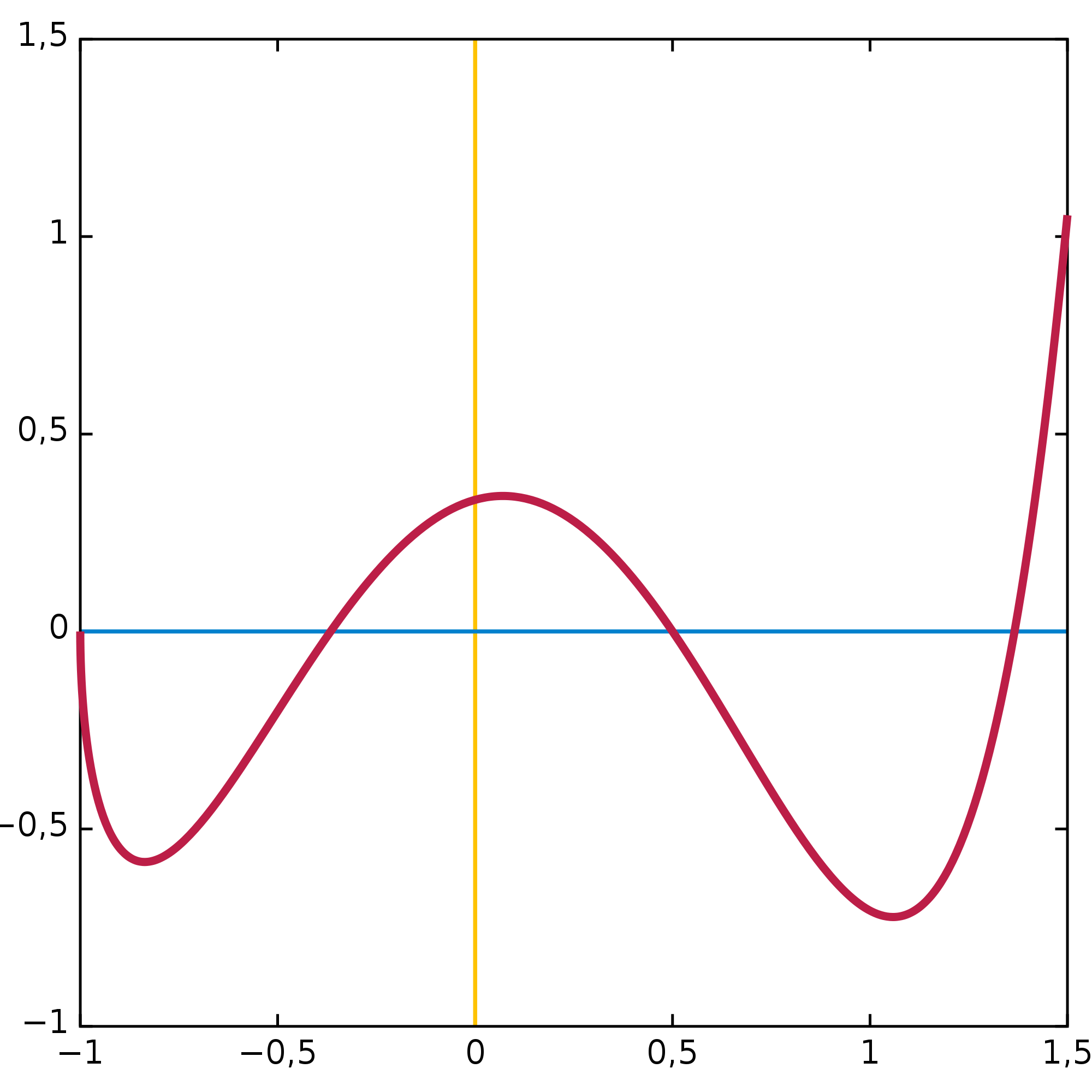
Att kolla på värde tabell när y värdet minskar, då måste kurvan gå neråt eller om y helt plötsligt gick från att minska till att öka på värde tabellen så går kurvan uppåt

Vad är en ny kurva här? Jag ser en enda kurva.

Laguna skrev:

Vad är en ny kurva här? Jag ser en enda kurva.

det finns väl 2 stycken kurvor. En på vänster sida och en på höger sida? Med värdetabell kan man se om linjen går upp eller ner. En metod att skriva ner en graf utan grafräknare

Det finns en linje

Varför vill du dela upp kurvan i vänster och höger?

Diagrammet säger mer än en värdetabell, tycker jag.

Laguna skrev:

Varför vill du dela upp kurvan i vänster och höger?

Diagrammet säger mer än en värdetabell, tycker jag.

Min lärare visade mig bara ett sätt att skriva ner en linje/diagram med värdetabell om man skulle behöva det under provtiden där grafräknare ej är tillåtet. Att dela upp kurvan till vänster och höger gjorde jag inte, det är ju bara 1 linje med 2 kurvor. Kurva betyder väl ''sväng'', detta diagrammet har 2 sväng

matematiskt är det kanske bättre att säga att den har flera minimi och maximi?

Aha, det är ordet kurva som ger problem. I verkliga livet är en kurva en sväng och inte flera, men i matematik är en kurva alla punkter (x,y) som ges av en funktion.

Så i din bild finns bara en kurva.

Menade du alltså tidigare att varje kurvavsnitt mellan två extrempunkter beskrivs av ett andragradspolynom?

Det stämmer inte.

Laguna skrev:

Menade du alltså tidigare att varje kurvavsnitt mellan två extrempunkter beskrivs av ett andragradspolynom?

Det stämmer inte.

Men om det  är en fjärdegradspolynom med flera ''kurvavsnitt'' varför beräknar man det som en andragradspolynom för det kommer ju finnas flera ''kurvavsnitt'' än det finns på en andragradspolynom?

När beräknar man det som ett andragradspolynom?

Laguna skrev:

När beräknar man det som ett andragradspolynom?

T.ex när man bryter ut x från x^3 -8x^2 + 5x = 0 

=> x^2 - 8x + 5 = 0

Blir det samma kurva på båda av dessa i grafen även om man bryter ut x ur x^3?

Om jag skrev q(x) = x^3 - 8x^2 + 5x = 0, måste man bryta ut x då (på grund av m)?

Eller t.ex p(x) = x^3 - 8x + 5

x(x²-8x+5) och x²-8x+5 är olika funktioner och deras kurvor ser olika ut, men du hittar nollställen till den förra genom att hitta nollställen till den senare.

Laguna skrev:

x(x²-8x+5) och x²-8x+5 är olika funktioner och deras kurvor ser olika ut, men du hittar nollställen till den förra genom att hitta nollställen till den senare.

Om det är olika funktioner varför bryter man ut funktionen från början om man vill ta reda på hur kurvan av x(x^2-8x+5) ser ut och inte x^2-8x+5?

 

men du hittar nollställen till den förra genom att hitta nollställen till den senare.

Ok, så att man kan använda funktionen av x^2-8x+5 för att senare beräkna funktionen av x(x^2-8x+5)?

Hur skulle det se ut isåfall?

Först vill man hitta nollställena, och då är det rätt metod.

Ville man veta något mer i det här fallet?

Laguna skrev:

Först vill man hitta nollställena, och då är det rätt metod.

Ville man veta något mer i det här fallet?

Bara att skriva ner x(x^2-8x+5) = 0 på en graf. Med beräkningsmetod. 

Som jag förstår är svaren för nollställena av funktionen x(x^2-8x+5): x=0,  x=4-sqrt(11)  x=4+sqrt(11), där ''x=4-sqrt(11)  x=4+sqrt(11)'' är nollställen från funktionen x^2-8x+5, men också x(x^2-8x+5)

Och den beräknades genom att använda pq metoden för den andra funktionen x^2-8x+5.

Det sista som behöver göras nu är att rita ner grafen och se om den stämmer med kurvan x(x^2-8x+5)