Potentialskillnaden mellan två punkter
Tja, se del b nedan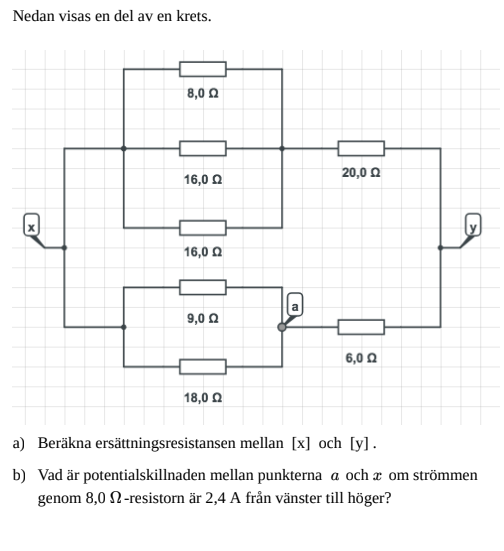
Jag började att hitta spänningen över 8-ohms resistorn, sedan hitta ers-resistansen till den övre parallellkopplingen och använde ohms lag för att hitta den totala strömmen i kretsen.
2.4*8= 19.2 (spänningen över den övre parallellkopplingen)
(2/16)+(2/16) = 4/16 sedan inverterar vi och får att ers-resistansen för den övre parallellkopplingen är 4 ohm. 19.2 = I * 4 så då borde I = 19.2/4 som är 4.8
Jag förväntar att potentialskillnaden mellan x och a är spänningen över den nedre parallellkopplingen. Jag hittar ersättningsresistansen för den nedre parallellkopplingen.
(2/18) + (1/18) = 3/18 sedan inverterar vi och får 18/3 = 6. Spänningen över parallellkopplingen bör då vara 6 * 4.8 = 28.8V. Facit säger 58V och det är bara 28.8*2 och avrundat, så jag tror ju inte jag är helt ute och cyklar. Fattar inte vad jag bör gjort annorlunda genom min beräkning.
Vart gjorde jag fel och hur borde jag gjort istället?
Mvh
Lösning: Tänkte inte att strömmen går från x till y, tänkte att den går runt om som klockan/dvs det är en parallellkoppling mellan x och y.
Jag tror du räknat rätt, nästan hela vägen.
Det är lite svårt att följa, men jag tror du beräknat strömmen korrekt till 4,8 A genom den övre ersättningsresistansen, alltså den jag har benämnt Ra. Sedan utgår du ifrån att strömmen genom den nedre (mitt Rb) är densamma. Det är den inte, eftersom Ra <> Rb.
Så här har jag räknat, lite spontant.
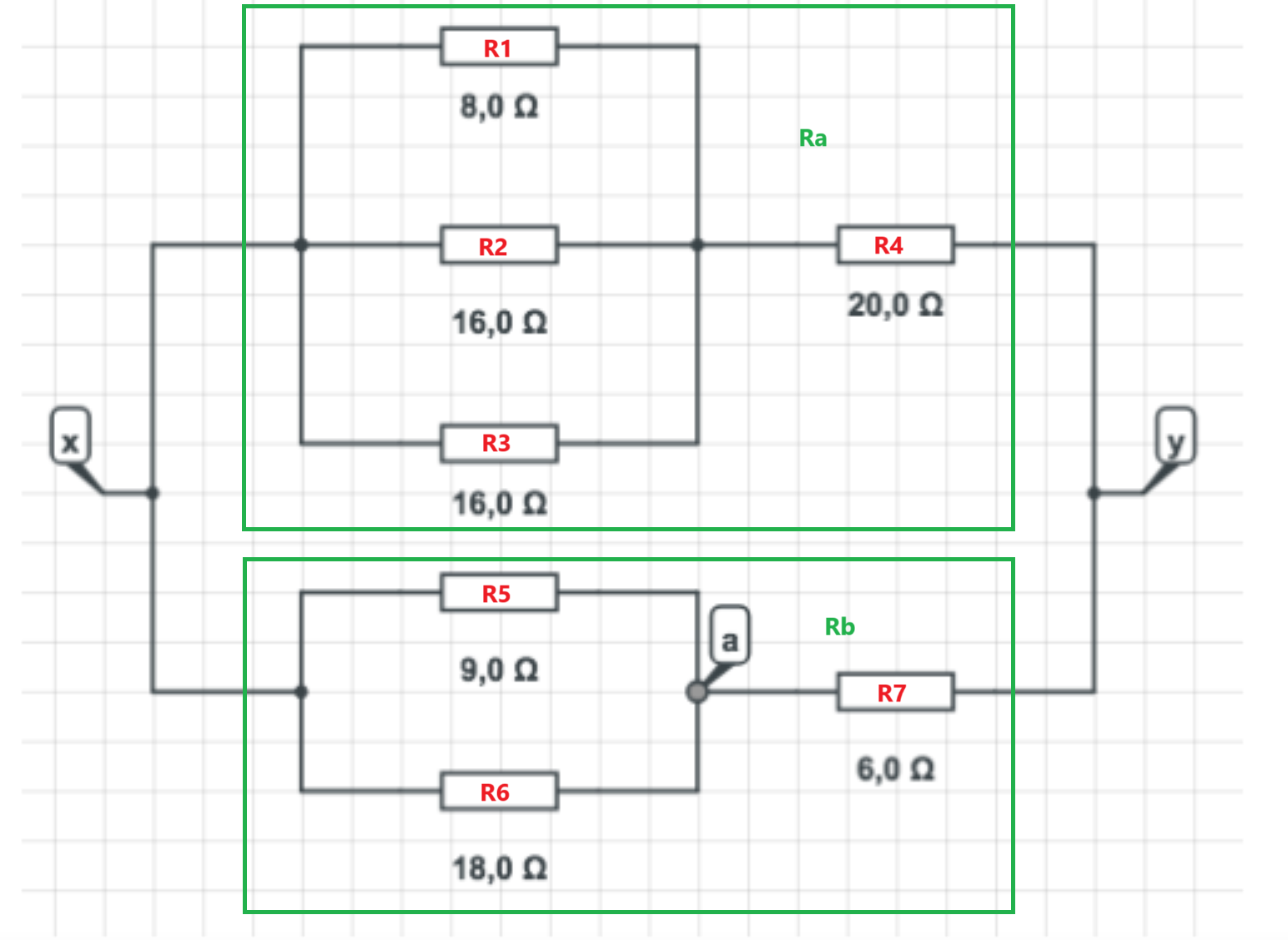
R2 || R3 = 8 Ω
R1 || R2 || R3 = 4 Ω
Ra = R1 || R2 || R3 + R4= 24 Ω
R5 || R6 = 6 Ω
Rb = R5 || R6 + R7= 12 Ω
Ersättningsresistansen är alltså: R = Ra || Rb = 8 Ω
Uppgiften ger 2,4 A genom R1. Eftersom R1 = R2 || R3 får vi 2,4 A genom R2 || R3, så totalt 4,8 A genom Ra.
Då kan vi räkna ut potentialen mellan x och y:
U(xy)=24*4,8=115,2 V
Eftersom Ra och Rb är parallellkopplade över xy så är spänningen över Rb=115,2 V.
Denna spänning kommer att fördela sig över R5 || R6 och R7 som 6 Ω förhåller sig till 6 Ω, alltså som 1:1.
Potentialen i a relativt x är således 115,2/2 ≈ 58 V.
Hej, jag fattar din lösning: Hitta spänningen över hela övre delen, det är den samma som spänningen i den undre, och den nedre parallellkopplingens ers-resistans är det samma som R7. VSV U(ax) = spänningen i den hela övre delen delat på två. Dock fattar jag fortfarande inte varför min metod inte funkar.
Vi har hittat spänningen 115,2 V och ersättningsresistansen 8 Ω.
Den totala strömmen genom kretsen är alltså 115,2 / 8 = 14,4 A.
Strömmen över den övre delen har du beräknat till 4,8 A, så då går det 9,6 A genom den nedre.
Nu kan du använda ohms lag för att beräkna spänningen över R5 || R6: 6*9,6 = 57,6 V
