Potential av ett vektorfält.

Försöker lösa potentialen av följande vektorfält:

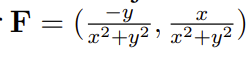
Facit säger att potentialen blir följande (utan motivering):

Jag ser att vid integrering av x-komponenten vid avseende på x får man -arctan(x/y) + c(y) och dessutom arctan(y/x) + c(x) om man kollar på y-komponenten. Jag antar att jag på något sätt (efter använding av polära koordinater) ska få arctan(rsin(t)/rcost(t)) = arctan(tan(t)) = t. Däremot kommer jag inte längre än så. Tack för hjälp!

Hej och välkommen till Pluggakuten!

$θ$ är definierad som $θ = a r c \tan (\frac{y}{x})$ , alternativt kan detta ses från definitionerna av x och y med avseende på r och $θ$ .

Från integreringarna har vi att potentialen är lika med just detta uttryck, därmed $θ$ .

Calle_K skrev:
Hej och välkommen till Pluggakuten!

$θ$ är definierad som $θ = a r c \tan (\frac{y}{x})$ , alternativt kan detta ses från definitionerna av x och y med avseende på r och $θ$ .

Från integreringarna har vi att potentialen är lika med just detta uttryck, därmed $θ$ .

Tack!

Förstår dock inte hur detta blir potentialen eftersom när jag integrerar upp $\frac{- y}{x^2 + y^2}$ med avseende på x får jag -arctan(x/y) + c(y) vilket inte blir rätt.

Det kan vara lite klurigt när man ser det första gången, men

$\arctan(\frac{1}{x})=\frac\pi2-\arctan(x)$ då $x>0$

Och integrationskonstanten, t.ex. $\pi/2$ , är godtycklig.

D4NIEL skrev:
Det kan vara lite klurigt när man ser det första gången, men

$\arctan(\frac{1}{x})=\frac\pi2-\arctan(x)$ då $x>0$

Och integrationskonstanten, t.ex. $\pi/2$ , är godtycklig.

Tack så mycket! Nu förstår jag.

Svara

Visa senaste svar