Potenslagar
hejsan
jag har fastnat med min beräkning i denna uppgift a)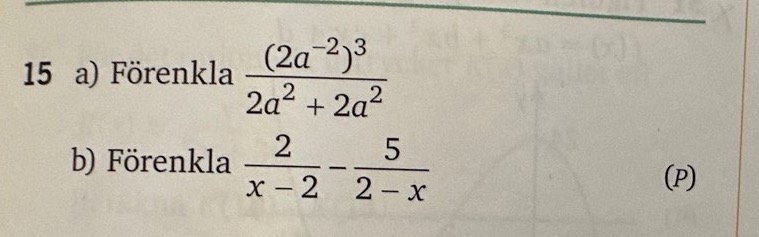

Använd att för och .
Hur blir det när det står 4a2 i nämnaren ?
basen i täljaren är 2
och på b)
så försökte jag multiplicera första termen med (-1) i täljaren och nämnaren.
För att på så vis få samma nämnare i första och andra termen.
jag fick svaret till -7/2-x
Basen är både i täljare och nämnare. I en potens så är basen och exponenten. Det som står framför, alltså i det här fallet och , är koefficienter, eller bara tal. Alltså så här:
.
På b) så tycker jag du har gjort rätt. Jag får samma svar.
Svaret på a) ska vara 2a-8
Svaret på b) på så ska det vara 7/x-2
Biorr skrev:Svaret på a) ska vara 2a-8
Svaret på b) på så ska det vara 7/x-2
Okej, jag ser nu att du missat att i första steget i a) så är . Då får man i slutet
istället.
Notera också att
, så ditt svar är samma som facit. Ser du varför?
på B)
Är det för att man istället har multiplicerat med (-1) på den andra termens täljare och nämnare dvs 5/(2-x) ?
på a)
hur ska man veta att man ska utveckla täljaren och sedan använda den typen av potenslag.
än att göra som man gjorde i börja där man använde en annan potenslag?
.
Jag förstår inte din fråga om a). Det finns inte så mycket annat att göra än att utveckla täljaren och förenkla nämnaren. Gör man det ser man att man kan förenkla ytterligare enligt .
Biorr skrev:på a)
hur ska man veta att man ska utveckla täljaren och sedan använda den typen av potenslag.
än att göra som man gjorde i börja där man använde en annan potenslag?
Tänker att man bara får köpa att det är så potenslagarna lyder. Tror att du kanske råkat glömma/blanda ihop lite bara. Egentligen måste man ju inte skriva ut alla om det är det du tänker på.. (det är dock en bra grej att göra när man vill förtydliga/förklara såhär såklart!)
Räcker bara att följa rätt potenslag för fallet: (Men då är det viktigt att man gör rätt! )
som jag tror det råkade bli i detta fallet :)



