Potensekvationer

Det ska vara x^2 + 2*x + 1 istället för x^2 + x*x + 1 ... men din metod är i sig själv inte lämplig.

Taylor skrev:

Det ska vara x^2 + 2*x + 1 istället för x^2 + x*x + 1 ... men din metod är i sig själv inte lämplig.

Vilken metod är lämplig? 

Gör kvadratrot direkt i början.

Taylor skrev:

Gör kvadratrot direkt i början.

Oh. Ok, då fattar jag. Men varför funkar inte metoden i början, betyder det egentligen inte samma sak? 

Du gjorde ju ett slarvfel på din omväg.

Taylor skrev:

Du gjorde ju ett slarvfel på din omväg.

Vart då

se ovan

Taylor skrev:

se ovan

jag förstår inte riktigt, ska man inte använda denna formel: 

Är det plustecknet mellan paranteserma som jag missar?

Det ska vara

x^2 + 2*x + 1 = 16

istället för

x^2 + x*x + 1 = 16

.

Omvägen du tar kräver att du använder pq-formeln eller abc-formeln. Det är mycket enklare att ta $\pm \sqrt{}$ direkt. 

Dessutom använde du kvadreringsregeln fel, det gäller att: ${(a\pm b)}^2=a^2\pm 2ab+b^2$.

Tillägg: 6 nov 2022 11:02

Det finns till och med en metod där man försöker göra om ena ledet till en kvadrat för att det är just så enkelt då. Sök på "kvadratkomplettering".

Du verkar vara extremt nyfiken hur man kan lösa det på ett alternativt sätt. 

OK, jag har inget emot att du är nyfiken, jag gillar det faktiskt.

Jag visar dig tre alternativa vägar att lösa en andragradsekvation, 2 av de tillhör matematik 2 och den tredje tillhör varken. Den kan väl antas egentligen vara matematik 1 men jag har svårt för hur något på denna nivån skulle kunna resonera på detta sättet. 

Metod ett #1 - Kvadratkomplettering

Jag expanderar och flyttar över 16, så du får en inblick hur man gör. Om jag kör på nu direkt är jag i princip klar eftersom VL är redan en perfekt kvadrat.

$x^2+2x-15=0$

Kvadreringsreglerna säger att $(a+b)^2=a^2+2ab+b^2$. Denna är extra intressant eftersom vi har en positiv $x^2$ och positiv koefficient framför $x$-termen. Kikar vi nu noga ser vi att vi vill enligt kvadreringsregeln ha det på form:

$(x+c)^2$. Från termen i mitten, nämligen $2ab$ så får vi efter att vi låter $a=x$ att $b=1$. Nu har vi:

$(x+1)^2$, men denna kvadraten kommer producera $b^2$, så den måste vi dra bort:

$(x+1)^2-1^2-15$

Nu har vi $(x+1)-16$, och vill vi nu lösa ekvationen så släger vi över konstanten:

$(x+1)^2=4^2 \iff x = -1 \pm 4$

Metod #2 - PQ/ABC

Man härleder PQ-formeln mha kvadratkomplettering. Det finns en annan variant som Naytte kallar ABC formeln, det är i princip samma sak bara att PQ är en mer "förenklad" form. 

PQ-formeln säger att om vi har $f(x)=x^2+px+q$ så ges x av:

$x = - \dfrac{p}{2} \pm \sqrt{(\dfrac{p}{2})^2-q}$

ABC-formeln (används i USA) säger att om vi har $f(x)=ax^2+bx+c$ så ges $x$ som:

$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$

Metod #3

Antag att:

$x^2-(-2x)-15 = (x-x_1)(x-x_2)$ - från faktorsatsen.

Efter vi expanderat och snyggat till det lite så fås:

$x^2+2x-15=x^2-(x_1+x_2)x+x_1x_2$

Vi söker $x_1$ och $x_2$ sådant att: 

$x_1+x_2=2$ och $x_1x_2=-15$

Mittpunkten ges som $M=-1$

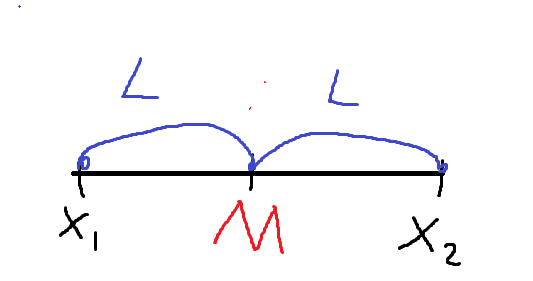Från bilden ser vi nu att:

$x_1=-1-L$ och $x_2=-1+L$

Vi hade från tidigare att $x_1x_2=-15$, varav: 

$(-1-L)(-1+L)=-15$ - använd konjugatregeln:

$1-L^2=-15 \iff L=  4$ - en längd är aldrig negativ.

$x_1 = -1-L = -5$, $x_2 = -1+L = 3$.