Polynomekvation och komplexa talplanet
När lösningarna till ekvationen z^3−4z^2+5z=0 anges som punkter i det komplexa talplanet kan en cirkel ritas som går genom alla punkterna. Bestäm cirkelns radie.
Jag kom till detta men förstår inte hur man beräknar radien från de punkterna.

junkol skrev:När lösningarna till ekvationen z^3−4z^2+5z=0 anges som punkter i det komplexa talplanet kan en cirkel ritas som går genom alla punkterna. Bestäm cirkelns radie.
Jag kom till detta men förstår inte hur man beräknar radien från de punkterna.
Uppgiften blir myckt enklare att lösa om du ritar in de tre komplexa talen i det komplexa talplanet. Lägg upp bilden här - och skaffa dig ett rutat block att räkna matte i!
Smaragdalena skrev:junkol skrev:När lösningarna till ekvationen z^3−4z^2+5z=0 anges som punkter i det komplexa talplanet kan en cirkel ritas som går genom alla punkterna. Bestäm cirkelns radie.
Jag kom till detta men förstår inte hur man beräknar radien från de punkterna.
Uppgiften blir myckt enklare att lösa om du ritar in de tre komplexa talen i det komplexa talplanet. Lägg upp bilden här - och skaffa dig ett rutat block att räkna matte i!

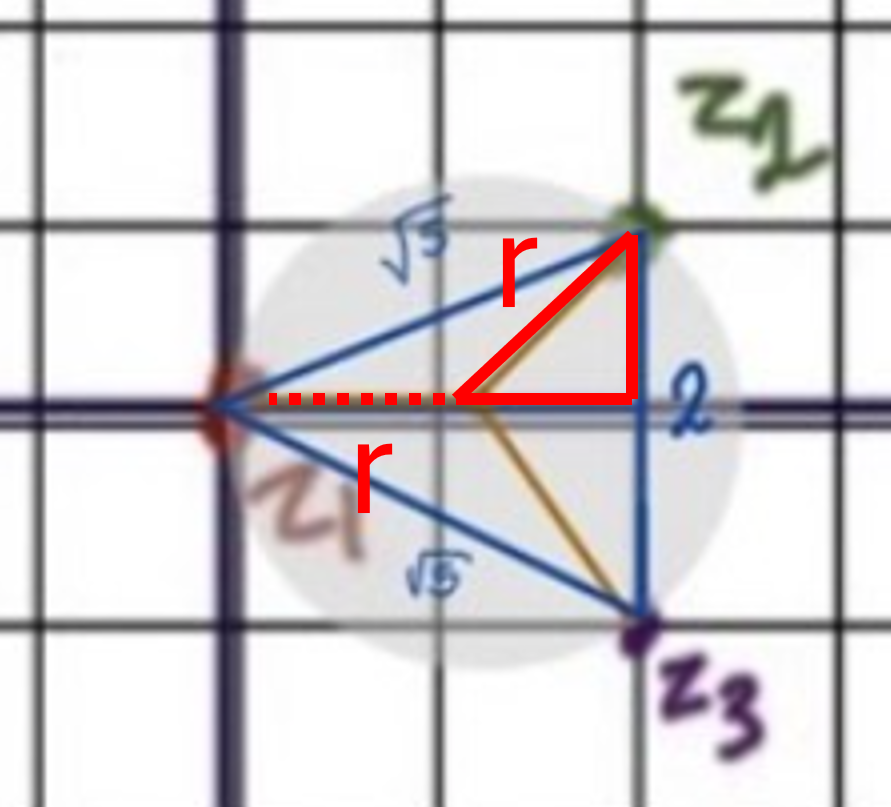
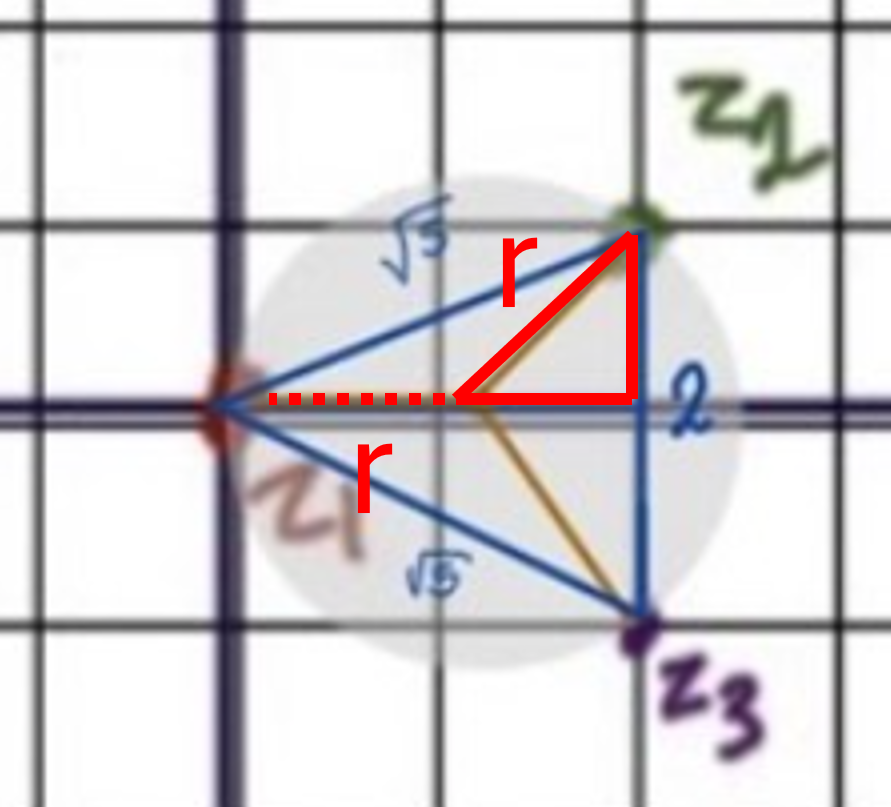
Snyggt! Kan du nu rita ut ungefär var cirkelns mittpunkt borde ligga för för att cirkeln ska kunna tangera alla lösningspunkter, så ser du hur du ska beräkna radien.
JohanF skrev:Snyggt! Kan du nu rita ut ungefär var cirkelns mittpunkt borde ligga för för att cirkeln ska kunna tangera alla lösningspunkter, så ser du hur du ska beräkna radien.
Ja bra!
Du har listat ut att mittpunkten måste ligga på x-axeln, i punkten (x,y)=(r,0). Då kan du använda avståndsformeln för att lista ut vad r ska vara.
Ser du hur du kan göra?
JohanF skrev:Ja bra!
Du har listat ut att mittpunkten måste ligga på x-axeln, i punkten (x,y)=(r,0). Då kan du använda avståndsformeln för att lista ut vad r ska vara.
Ser du hur du kan göra?
Är avståndsformeln samma som pythagoras sats?
JohanF skrev:Ja


Men här vet jag inte vad jag gjorde fel… radien ska väl vara 1.25
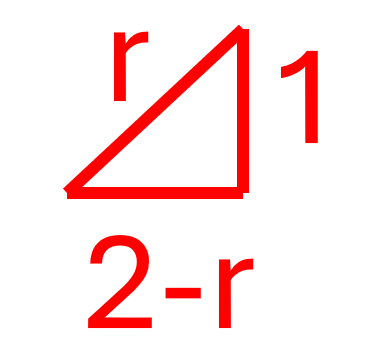
Ja, radien 2 är orimligt! (det kan man se i din figur). Det är triangels som jag ritade nedan som du ska räkna på. Ser du hur?
JohanF skrev:Ja, radien 2 är orimligt! (det kan man se i din figur). Det är triangels som jag ritade nedan som du ska räkna på. Ser du hur?
Jaa! ok.
Men hur kan jag räkna radien med två okända värden?
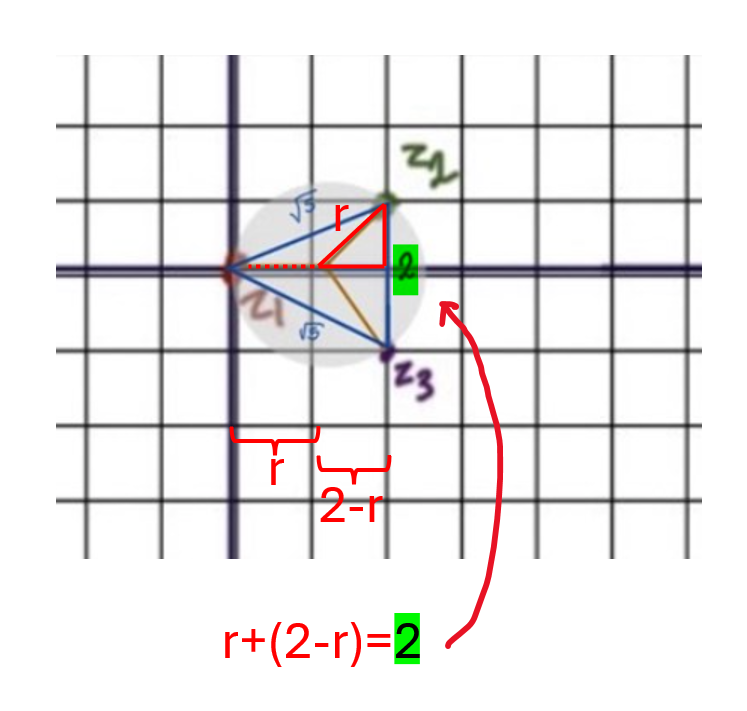
Kan du se du att det blir såhär?
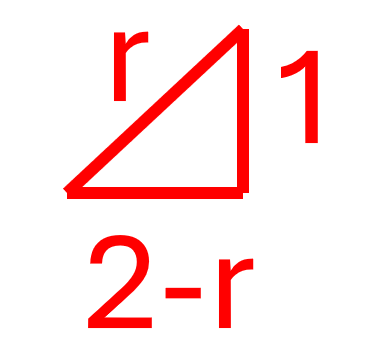
JohanF skrev:Kan du se du att det blir såhär?
asså jag känner mig så dum, kan fortfarande inte förstå varför det blir 2-r?
Neeej, du behöver inte känna så! Jag får förklara lite bättre bara.
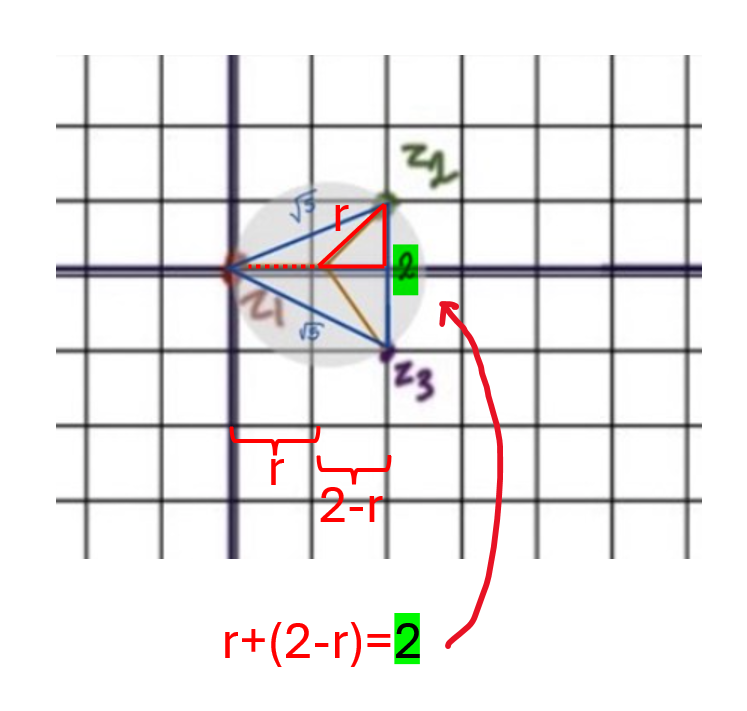
JohanF skrev:Neeej, du behöver inte känna så! Jag får förklara lite bättre bara.
Tack så jättemycket!!! Nu förstår jag;)
Va bra! Vad får du för värde på radien?