polynomekvation K
 Jag känner mig lite osäker på hur jag ska gå till väga här. Skulle någon kunna ge mig ett tips på hur jag kan börja lösa denna uppgiften. grad två" betyder det z^2 eller
Jag känner mig lite osäker på hur jag ska gå till väga här. Skulle någon kunna ge mig ett tips på hur jag kan börja lösa denna uppgiften. grad två" betyder det z^2 eller
"Av grad två" innebär att det ska vara ett andragradspolynom, dvs. ett polynom på formen .
Att är en rot till en ekvation innebär att löser ekvationen. Känner du till vad nollställesform innebär för ett polynom?
naytte skrev:Känner du till vad nollställesform innebär för ett polynom?
Nej, jag fattar inte.
Ett andragradspolynom med nollställen och kan skrivas på formen .
Kan du komma vidare med det? :)
Reella koefficienter --> studera komplexkonjugatet.
Skulle du kunna utveckla ditt svar lite mer, @Trinity2?
naytte skrev:Skulle du kunna utveckla ditt svar lite mer, @Trinity2?
Om ett polynom har reella koefficienter är lösningarna parvis konjugerade.
Då en rot är 1+2i är den andra 1-2i
Ett exempel på polynomekvation ges därmed av (z-(1+2i))(z-(1-2i)) = z^2-2 z+5 = 0
Sedan kan godtyckliga multipler av detta användas.
Nu när jag sitter vid datorn kan jag skriva lite mer utförligt också.
Nollställesform är inget som är unikt för andragradspolynom. Man kan faktiskt skriva om alla polynom, oavsett grad, på formen . Ett lite konsicare sätt att skriva detta på är:
Detta kallas för pi-notation, vilket du kan jämföra med sigma-notation ()
är koefficienten på -termen av högst grad och är polynomets nollställen. Att man kan skriva om polynom på detta sätt är en konsekvens av faktorsatsen.
Tack för hjälpen Trinity2 och Naytte. Jag har noterat och ska studera detta lite djupare, det var bra svar o beskrivningar.
Min matte lärare förklarade en annan lösning, som jag använde mig av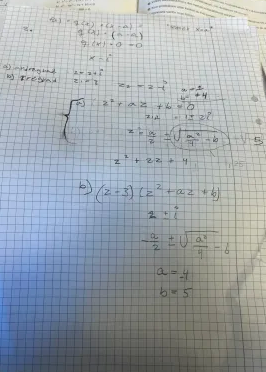 a) a=-2 o b=5
a) a=-2 o b=5
b)-4=a b=5



