Polynom och nollfaktorlagen

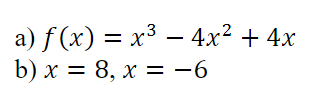
Hur lyder b) frågan egentligen?

i a) så kan du bryta ut ett x:

$x(x^2-4x+4)$, vet du hur man faktoriserar en andragradare?

Tips på b-uppgiften:

Låt g(x) vara ett polynom. Då har ekvationen g(x) = 0 lösningar vid x = 8 och x = -6 om dessa x-värden är nollställen till polynomet g(x).

Hur? 

jag fattar inte b uppgiften?

Vi tar ett exempel som ledtråd:

Ekvationen (x-3)(x+5) = 0 har enligt nollproduktmetoden lösningarna x = 3 och x = -5.

Detta eftersom när x = 3 så har första parentesen värdet 0 och när x = -5 så har andra parentesen värdet 0.

Är du med på det?

Kan du i så fall använda det tänket till b-uppgiften?

aha så att det blir: (x-8)(x+6), x=8 och x=-6

Shasha skrev:

aha så att det blir: (x-8)(x+6), x=8 och x=-6

Om du menar (x-8)(x+6) = 0 så blir det en ekvation och då är det rätt.

Om man faktoriserar andragradsekvation måste man välja pq formeln eller kan man bara jobba med kvadrerinsregel? Tänkte såhär

x(x^2−4x+4)

x((X-2)^2) för att om man använder pq

man kommer till att

x1=2 => (x-2)=0

x2=-2 => (x+2)=0

(x-2)(x+2)=x^2+2x-2x+2^2=x^2+4 vilket speglar inte de som var i parantes. 

Kan någon säga om jag har rätt? 

Ditt x1 stämmer, men inte ditt x2.

Lös ekvationen (x-2)² = 0 på papper så ser du det.