Polynom

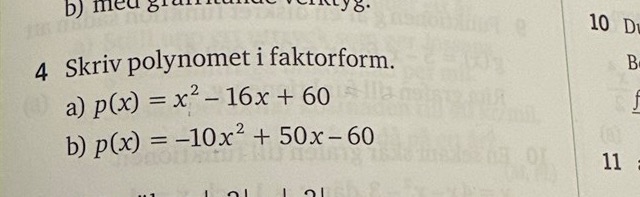
Hej! Vad har du gjort för arbete på uppgiften? 

Försökte med kvadrakomplettering och kvadreringsregeln.

pq-formel får ej användas i nuläget 

Biorr skrev:

Försökte med kvadrakomplettering och kvadreringsregeln.

pq-formel får ej användas i nuläget 

Kvadratkomplettering borde fungera i detta fall för att hitta funktionens nollställen. Tänk på att $(ax-b)^2 = ax^2 - 2abx + b^2$. Vad skulle $a$ och $b$ kunna vara i frågan?

Vet ej om detta är rätt

Biorr skrev:

Vet ej om detta är rätt

Det stämmer! Du kan alltid testa nollställena genom att lägga tillbaka dem i funktionen och dubbelkolla att det faktiskt blir 0. En mycket liten sak är dock mellan steget
$(x-8)^2 = -60 + 64$
till 
$(x-8)^2 = \pm 4$
Det blir inte $\pm 4$ förrän man tar roten ur
$(x-8)^2 = 4$
Här får vi att 
$x-8 = \pm \sqrt{4} = \pm 2$

Också, här är litet snabbknep för att faktorisera sådana här uttryck

För en andragradare som har formen $(x-r)(x-t) = x^2 - xr - xt + rt= x^2 - x(r+t) +rt$. Från nollproduktsmetoden ser vi att $r$ och $t$ är nollställena till andragradaren. Dessutom ser vi att $-(r+t)$ är koefficienten framför $x$ termen och $rt$ är konstanttermen. Alltså får vi att koefficienten framför x-termen är -(nollställena adderade) och konstanttermen är nollställena multiplicerade med varandra. 

Därför, när man ser ett uttryck, exempelvis $x^2-6x+8$ kan man ställa sig frågan, vilka två tal adderat till varandra blir 6 (alltså den negativa varianten av koefficienten framför x-termen) och multiplicerat blir 8? Antingen genom ekvationssystem eller att testa sig fram kan man få reda på att talen är 2 och 4. Då vet vi att $x^2 - 6x+8 = (x-2)(x-4)$. Ganska snabb och enkel metod för att faktorisera dessa uttryck om det är heltal i alla fall. 

Jag tycker detta är en bra grej att göra innan man börjar jobba med en uppgift för att kanske få en ide om vad svaret kan vara. Det kanske inte är metoden man ska använda när man faktiskt löser en uppgift i en bok eller på ett prov dock.