Planering av en lektion
Hej, vi har som projekt att göra en planering av en lektion om lilkformighet för matematik 2c,
jag har gjort planeringen som jag nu bifogar
men min fråga är att hur ska jag snygga till så att den blir bra planering
till exempel hur ska jag sätta tidtabell, och är syftet bra
behöver jag skriva något mer




Finns det några tips på vilken arbetssätt eleverna kan göra under lektionen
tack på förhand
Som verksam lärare vill jag betona att jag sällan har detaljerade planeringar för mina lektioner bortsett från ett övergripande mål och ett urval av problem/aktiviteter som jag respektive eleverna ska utföra.
Feedback för lektionsplaneringen är något beroende av om målet är att ha en realistisk planeringsstruktur man kan tillämpa som utövande lärare eller om lektionsplaneringen är en verktyg för att analysera och diskutera det teoretiska didaktiska problemet. Dessa står något i mortsats till varandra. Vid realism måste man hålla det kort och öppet, vid analys vill man ha det konkret och detaljerat.
Det du bör förbättra är
1. Konkretisera lektionen mål. Att lära sig om något är inte ett syfte eller ett mål. Du har i huvudet en ganska snäv bild av vad du vill åstadkomma och det är lämpligt att formulera de målen snarare än vaga mål som 'förstå vad likformighet är' då förståelse både är svårt att definiera och definitionsmässigt omöjligt för eleven att uppnå på en lektion. Konkreta mål kan vara:
- Att given bilder på två likformiga trianglar där ett par av motsvarande sidor är givna och ett par av motsvarande sidor är ofullständigt, kunna bestämma en okänd sida. Dvs konstruera och lösa ekvationer på formen a'/a = b'/b.
- Kunna avgöra vilka sidor som motsvarar varandra i två likformiga trianglar även när de är roterade eller speglade relativt varandra. Att sidorna som är längst motsvarar varandra, eller sidorna som är motstående samma vinkel motsvarar varandra.
- Kunna beskriva med en mening ett kriterie för när två trianglar är likformiga (specificera)
- Kunna SSS-metoden för att bevisa att trianglar är likformiga.
Sedan kan man såklart säga till eleverna att målet med lektionen är att förstå likformighet.
2. Du behöver med exempel och ett tidigare moment tydliggöra för eleverna vad motsvarande sidor är innan du går vidare. Och ge dem stöd för att avgöra vilka sidor som är/kan vara motsvarande utifrån form. Motsvarande sidor är ett sånt där begrepp som är mindre uppenbart än man tror och det är lätt att elever utvecklar missförståndet att motsvarande är säg sidor som är längst ner eller längst till höger (dvs är beroende av rotation) om man.
Du berör detta indirekt i uppg 2 men är bakvänt.
3. Din definition av likfomrighet är matematiskt korrekt men inte språkligt klar. Att säga saker som att likformiga trianglar är lika till form men har olika storlek kan vara mer konkret än att motsvarande sidor har samma förhållanden. Att kvoten av motsvarande sidor beskriver deras storleksförhållande kan även hjälpa att göra det intuitivare varför form och den här kvoten skulle höra ihop.
4. Uppgift 2 och 3 är fel. Man kan inte avgöra om två trianglar är likformiga endast från två par utan man måste ha alla tre par. Jämför den liksidiga triangeln 111 med den likbenta trianglen 221. Bryr vi oss bara om två sidor så tror vi att de är likformiga. Som men fördjupningsfråga är det här helt klart intressant men du behöver bestämma dig för om förmågan att avgöra likformighet genom SSS-kriteriet är något du vill ha med i lektionens mål.
Att kunna bestämma okända sidor i trianglar från likformighet är i de flesta program mer centralt än matematiska bevis så att prioritera ekvationslösning mer kan vara relevant.
5. Många elever har inte vana med bokstavsnotation AB för sträckan från A till B osv. Om målgruppen är vana vid den notationen kan du köra på det. Men om detta är första gången du skriver AB och EF så kan fokus hamna på det snarare än likformighet. Bokstavsnotation gör bara saker tydligare om man faktiskt förstår den.
6. Vad eleverna ska göra beror av arbetssätt. Jobbar de med ett läromedel bör det faktoriseras in i genomgången så att det hjälper dem att komma igång med uppgifterna. Om du ska ge alla uppgifter under lektionen så behöver det finnas en progression och variation i dem med en grad av variation.
7. Presentationsteknik. Har du möjlighet så gör gärna en power-point med bilder på trianglar. Att rita likformiga trianglar för hand och säga att de två trianglarna som uppenbart har olika form har samma form kan lätt bli förvillande.
Tillägg: 1 feb 2022 18:28
När du ger eleverna ett problem och en stund att lösa det. Bestäm dig för två saker:
1. Hur lång tid ska du ge dem. Att vänta tills det känns som att alla är klara fungerar inte. Bara säg 1min, är de klara är de klara. Du fortsätter oavsett.
2. Vad gör du när tiden är slut. Dvs hur bemöter du det som eleverna gjort med din uppgift som de gjort i par. Exempel på alternativ:
2a 'Okej, låt mig visa hur jag gör så kan ni säga om ni gjorde annorlunda.' (Dvs du försöker inte börja med interaktion)
2b. 'Okej kan Jonas längst bak förklara hur du gjorde på denna?' (Du börjar med interaktion)
2c. Svaret är 4... Moving on.
Medan växelverkan med klassen är viktigt så är diskurs bättre när frågor är öppna. Vi slutna frågor blir samtalet lätt en ledningskedja som inte ger så mycket. Gör en bra öppen fråga.
Detta är inte saker man nödvändigtvis skriver i planeringen men är saker man bör bestämma sig för så att man har trygghet i att man vet vad man vill göra.
hej, igen
tack så jättemycket,
du hade namnet sss-kriteriet, kan du ge mig ett exempel på en fråga som tillämpar detta problemet,
seden när det gäller " alla tre par", menar du att vi ska presentera 3 olika trianglar i stället för 2.
sedan är det bättre att ge tre exemplar och två uppgifter än att ge två exemplar och tre uppgifter
sista fråga
när det gäller tidsplanering, kan man planera så att under första timman ska man presentera temat och en eller två exemplar sedan under andra timman ska man presentera resten av exemplen och sedan ta upp uppgifterna. eller hur ska man göra då
tack på förhand
du hade namnet sss-kriteriet, kan du ge mig ett exempel på en fråga som tillämpar detta problemet,
seden när det gäller " alla tre par", menar du att vi ska presentera 3 olika trianglar i stället för 2.
sedan är det bättre att ge tre exemplar och två uppgifter än att ge två exemplar och tre uppgifter
När man jobbar med kongruens (lika form och storlek) så finns tre kriterier för kongruens hos trianglar som kallas SSS, SVS, och VSV. Dessa har motsvarigheter för likformighet och beskriver vad man behöver känna till för att avgöra om två trianglar är likformiga. En sats för/definition av likformighet för trianglar är att likformiga trianglar har samma interna vinklar: det kallar man för VVV-kriteriet (alla vinklarna är lika. Det andra är SSS-kriteriet vilket är att två trianglar är likformiga om och endast om alla motsvarande sidor har samma kvot, dvs att det finns ett skal-förhållande.
Det jag menar är att du måste och ska ge trianglarnas alla tre sidor om du ska kunna motivera att de är likformiga genom en numerisk beräkning av kvoterna. Om du bara tar två så har du lämnat öppet för följande nonsensresonemang:
Exempel (Liknande uppg 1,3,4): Låt mig visa att en liksidig triangel ABC och en oliksidig triangel A'B'C' är likformiga med metoden du givit
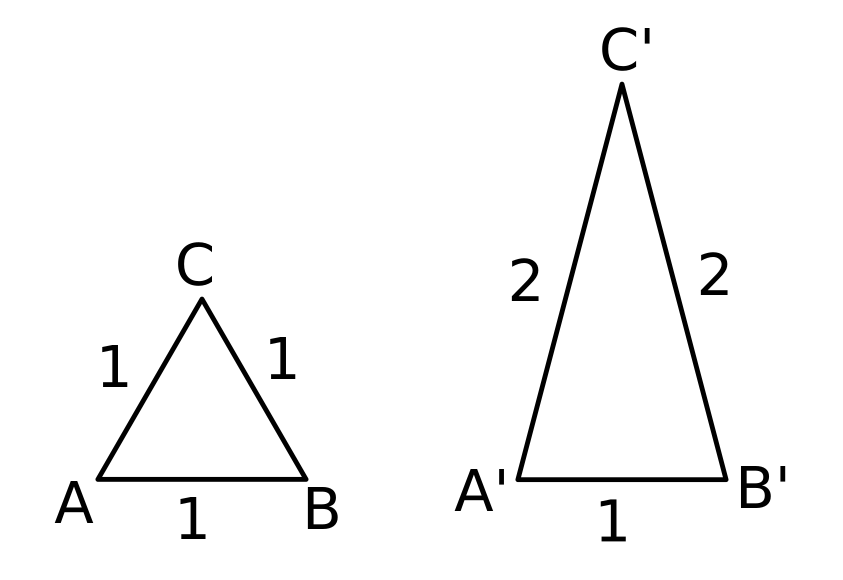
A'C' / AC = 2/1 = 2
C'B' / CB = 2/1 = 2
därmed
A'C' / AC = C'B' / CB
Därmed är de likformiga. Något saknas här eller hur?
Detta handlar dock om vad som är ett fullständigt matematiskt resonemang snarare än vad som är lämplig didaktik.
sista fråga
när det gäller tidsplanering, kan man planera så att under första timman ska man presentera temat och en eller två exemplar sedan under andra timman ska man presentera resten av exemplen och sedan ta upp uppgifterna. eller hur ska man göra då
tack på förhand
Beror på vad dina mål är och vad målgruppen är men låter väldigt utdraget. En timme fär väldigt lång tid. Med lite presentationsstöd så att man inte spenderar 15 min på att rita kan man avlägga alla dina exempel på 30-40 min men då har eleverna förstås inte lärt sig allt än, utan fått en orientering, och de kan göra någon aktivitet eller uppgiftssamling.
Jag skulle som sagt fokusera mer på ekvations-problemet och några fler exempel där än på att bevisa att specifika trianglar är likformiga.
Likformighet som koncept, att saker kan ha lika form men olika storlek och att det finns något som heter skala är något eleverna känner till från grundskolan så det kräver ingen introduktion och man har något att bygga på. De kan väldigt lite om det men de känner till själva grejen. Alla är exempelvis bekanta med skala och kartor, att en väg som är 2cm på en karta kan motsvara 2 km och likformighet i trianglar är en generalisering av det.
Hej, igen
tack så jättemycket
så jag måste ge alla trianglarnas sidor i mina exemplar
sedan ska jag fokusera mer på ekvations problemet
alltså hur vi sätter upp en ekvation utifrån det information vi får från uppgiften och sedan lösa den får att beräkna längden på den okända sidan
det som saknas är ju förhållandet mellan sidorna AB OCH A'B'
sedan när det gäller ekvations-problemet, menas detta att jag ska fokusera på problem såsom beräkna längden av sidan på en triangel : ex: som uppgift 4
Jag har nu skrivet ett exempel på ekvationsproblem
och undrar på om jag gör rätt



