Periodens påverkan på funktion
Hej!
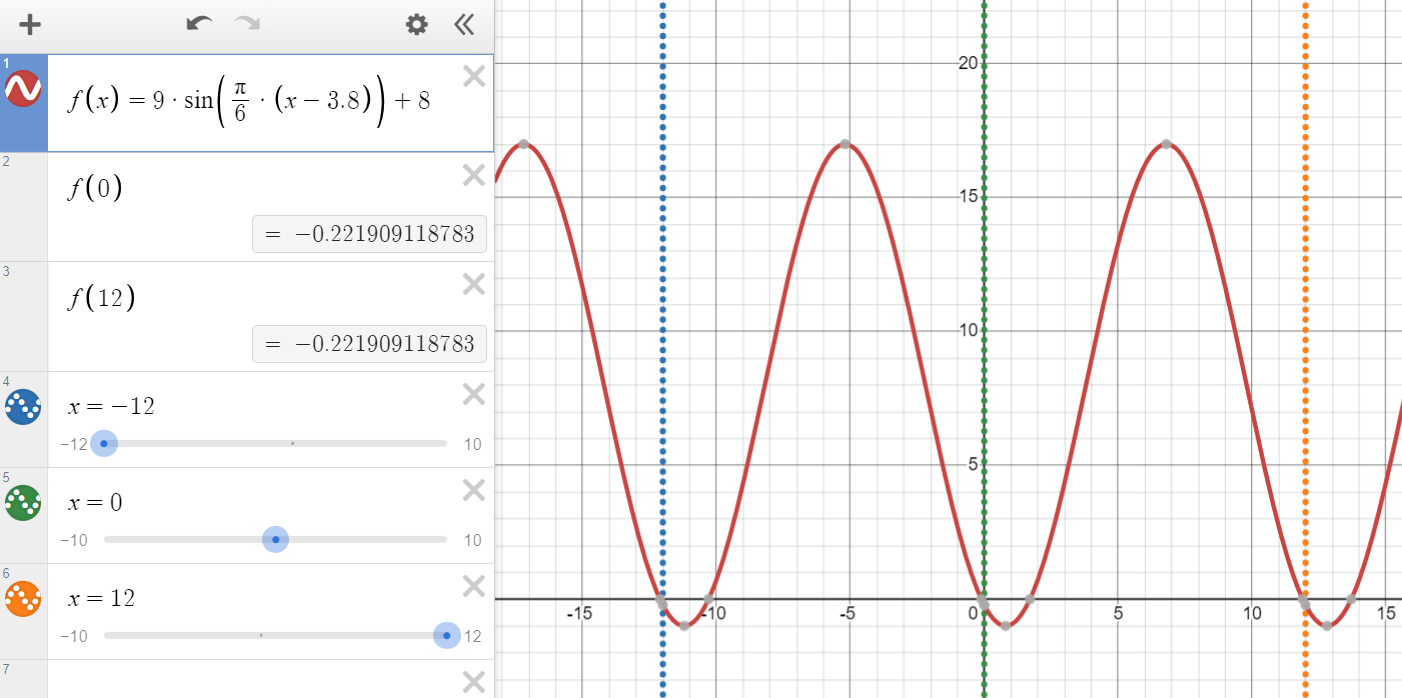
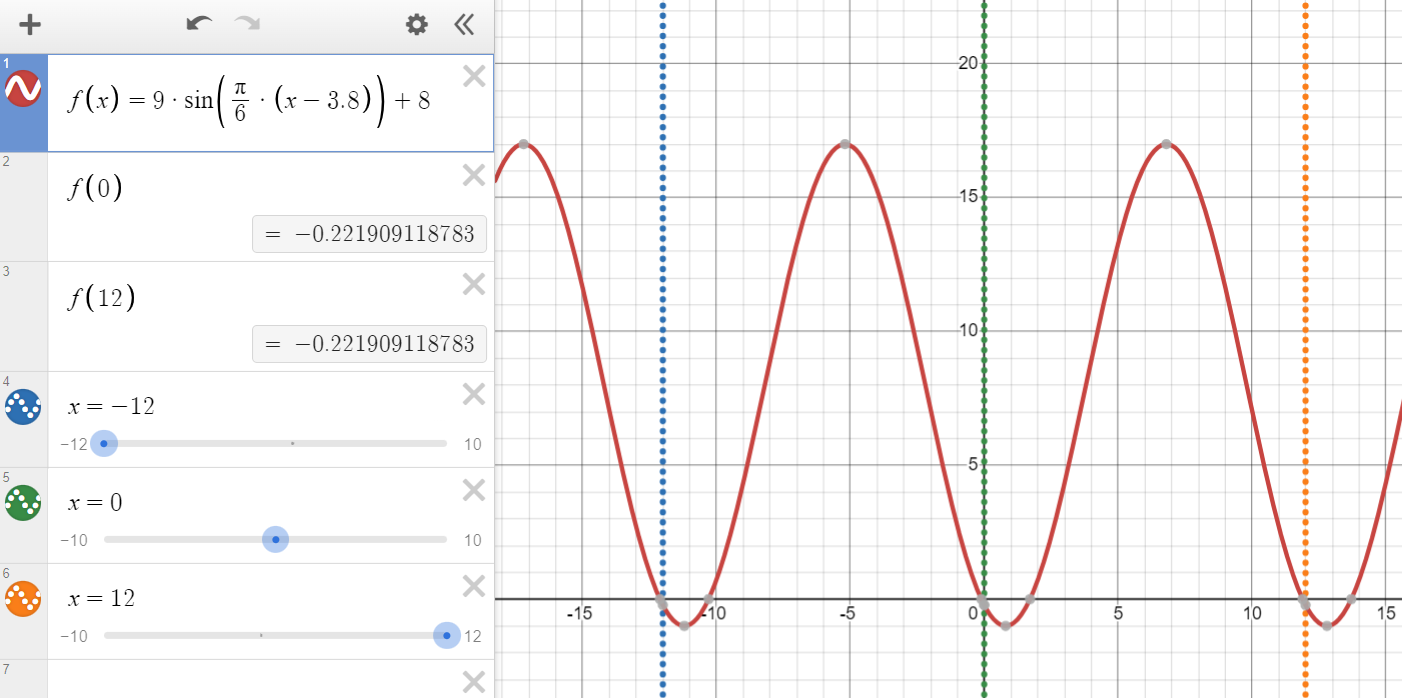
Jag fattar inte hur perioden påverkar på en trigonometrisk funktion. Här har ni exempel:

Liksom när ska perioden vara en del av funktionen? När är den inte en del av funktionen? Vad betyder det om den inte är eller är en del av funktionen?
Med "en del av funktionen" menar jag att perioden integreras med vinkeln och inte står utanför paranteserna.
Sinus har ju en period på radianer. Så om det inre uttrycket ökar eller minskar med 2π så får du samma värde på y.
Vi kan skriva om det lite grann:
Nu är det ganska lätt att se att om x=0 blir uttrycket .
Om x=12 blir uttrycket 2π större:
För just dessa exempel blir för alla x=12n där n är ett reellt tal. Där har du din period.
Tillägg: 25 jun 2024 10:14
Slarvfel av mig! Det skall vara "där n är ett heltal".
sictransit skrev:Sinus har ju en period på radianer. Så om det inre uttrycket ökar eller minskar med 2π så får du samma värde på y.
Vi kan skriva om det lite grann:
Nu är det ganska lätt att se att om x=0 blir uttrycket .
Om x=12 blir uttrycket 2π större:
För just dessa exempel blir för alla x=12n där n är ett reellt tal. Där har du din period.
Tack för svaret!
Dock förstår jag inte vad ni menar..
Vad är det du menar med "integreras med vinkeln"? Kan du ge några exempel?
Laguna skrev:Vad är det du menar med "integreras med vinkeln"? Kan du ge några exempel?
Jag har gett exempel i bilden ovan, liksom ibland multiplceras perioden in i vinkeln och ibland står perioden utanför vinkeln...
hoppas det blir tydligare
Nej, vad menar du med "multipliceras perioden in i vinkeln"?
... liksom ibland multiplceras perioden in i vinkeln och ibland står perioden utanför vinkeln...
Menar du att man t ex ibland skriver sin(3(x+10o)) och ibland sin (3x+30o)?