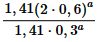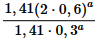Pendel; mätningar, pendelns svängningstid

Der vore intressant att se diagrammet som visar T som funktion av L. 

Vilka värden fick du på dina "kvoter"?

Hej och välkommen till Pluggakuten!

Du har ju förmodligen observerat att det verkar finnas ett matematiskt samband mellan T och l i din graf, eller hur? Men kanske svårt att se exakt vilket sambandet är. Utifrån de kvoter du räknat ut får man en ledtråd.

Antag att sambandet mellan T och l skulle ha varit proportionellt, dvs T= kl. Vad skulle din kvot ha blivit då?

Dr. G skrev:

Der vore intressant att se diagrammet som visar T som funktion av L. 

Vilka värden fick du på dina "kvoter"?

Ja, absolut!

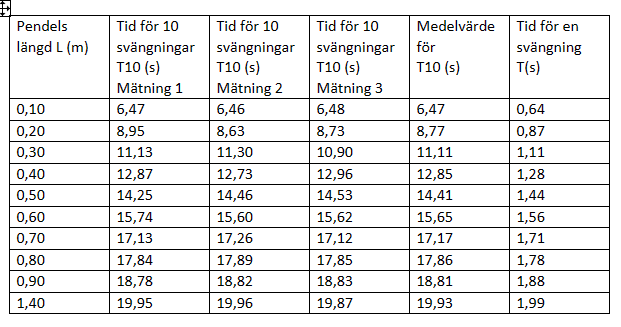
Det här tabellen från laborationen

Och det här är kvoterna jag fick, vad jag vet så skulle man använda sig av en ekvationen som jag håller på att klura över hur den funkar.

JohanF skrev:

Hej och välkommen till Pluggakuten!

Du har ju förmodligen observerat att det verkar finnas ett matematiskt samband mellan T och l i din graf, eller hur? Men kanske svårt att se exakt vilket sambandet är. Utifrån de kvoter du räknat ut får man en ledtråd.

Antag att sambandet mellan T och l skulle ha varit proportionellt, dvs T= kl. Vad skulle din kvot ha blivit då?

Hej!

Så det är lite som y =kx? 

Jag märkte också att man skulle använda sig en formel som jag passar på att fråga om också.Tror du att man kan då i det här fallet använda sig av den formeln de använder i instruktionerna T=k(roten ur L)? Att man först räknar ut kvoterna som du nämnde, sedan så tar man värdet in i formeln. Om jag har förstått det rätt.

Dr. G skrev:

Der vore intressant att se diagrammet som visar T som funktion av L. 

Vilka värden fick du på dina "kvoter"?

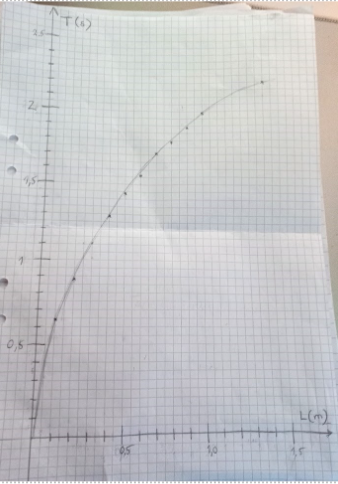
Här är diagrammet också :)

Jag tror du redan vet vilket sambandet är, dvs $T=k·\sqrt{l}$, eftersom den finns med i formelsamlingen 

Jag tror såhär om labben, om man inte först tjuvkikar i formelsamlingen, utan istället antar att du inte har en aning om sambandet före du genomför labben.

1. Du mäter, och ritar din graf över olika $T$ för olika $l$.

2. Du observerar i grafen att det ser ut att finnas något slags matematisk samband mellan T och l, men du kan inte riktigt se hur sambandet är.

3. Du resonerar vidare. Kanske sambandet kanske skrivas $T=k·l^a$, men du vet fortfarande inte värdet på exponenten $a$.

4. Värdet på exponenten $a$ kan undersökas med de kvoter som du räknat ut

$kvot=\frac{T_{dubbel}}{T}=\frac{k·{\left(2l\right)}^a}{k·l^a}=\frac{2^a{l}^a}{l^a}=2^a$

Medelvärdet på dina kvoter ser ut att bli ungefär 1.4 (du ser ut att ha räknat lite fel när du räknade ut medelvärdet på kvoterna). Vad får du alltså för värde på exponenten $a$?

JohanF skrev:

Jag tror du redan vet vilket sambandet är, dvs $T=k·\sqrt{l}$, eftersom den finns med i formelsamlingen 

Jag tror såhär om labben, om man inte först tjuvkikar i formelsamlingen, utan istället antar att du inte har en aning om sambandet före du genomför labben.

1. Du mäter, och ritar din graf över olika $T$ för olika $l$.

2. Du observerar i grafen att det ser ut att finnas något slags matematisk samband mellan T och l, men du kan inte riktigt se hur sambandet är.

3. Du resonerar vidare. Kanske sambandet kanske skrivas $T=k·l^a$, men du vet fortfarande inte värdet på exponenten $a$.

4. Värdet på exponenten $a$ kan undersökas med de kvoter som du räknat ut

$kvot=\frac{T_{dubbel}}{T}=\frac{k·{\left(2l\right)}^a}{k·l^a}=\frac{2^a{l}^a}{l^a}=2^a$

Medelvärdet på dina kvoter ser ut att bli ungefär 1.4 (du ser ut att ha räknat lite fel när du räknade ut medelvärdet på kvoterna). Vad får du alltså för värde på exponenten $a$?

Tack så jätte mycket för att du svarade på min fråga!

Jag prövade de stegen du skrev upp och jag tog ett exempel utifrån kvoten: 

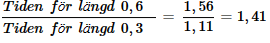
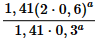
Om jag räknade rätt då fick jag det till 4.

Har jag förstått det rätt?

Jag prövade att räkna om medelvärdet och jag fick till det till 1,402 som du sa 1,4. Jag hade adderat det fel på miniräknaren. 

Fysik321 skrev:

JohanF skrev:

Jag tror du redan vet vilket sambandet är, dvs $T=k·\sqrt{l}$, eftersom den finns med i formelsamlingen 

Jag tror såhär om labben, om man inte först tjuvkikar i formelsamlingen, utan istället antar att du inte har en aning om sambandet före du genomför labben.

1. Du mäter, och ritar din graf över olika $T$ för olika $l$.

2. Du observerar i grafen att det ser ut att finnas något slags matematisk samband mellan T och l, men du kan inte riktigt se hur sambandet är.

3. Du resonerar vidare. Kanske sambandet kanske skrivas $T=k·l^a$, men du vet fortfarande inte värdet på exponenten $a$.

4. Värdet på exponenten $a$ kan undersökas med de kvoter som du räknat ut

$kvot=\frac{T_{dubbel}}{T}=\frac{k·{\left(2l\right)}^a}{k·l^a}=\frac{2^a{l}^a}{l^a}=2^a$

Medelvärdet på dina kvoter ser ut att bli ungefär 1.4 (du ser ut att ha räknat lite fel när du räknade ut medelvärdet på kvoterna). Vad får du alltså för värde på exponenten $a$?

Tack så jätte mycket för att du svarade på min fråga!

Jag prövade de stegen du skrev upp och jag tog ett exempel utifrån kvoten: 

 

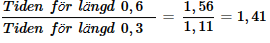
Om jag räknade rätt då fick jag det till 4.

 

Har jag förstått det rätt?

Jag prövade att räkna om medelvärdet och jag fick till det till 1,402 som du sa 1,4. Jag hade adderat det fel på miniräknaren. 

Jag tror det är nån detalj som fortfarande är oklar för dig, vi får bena i det lite till. Såhär:

Antag att $T$ hade varit proportionell mot $l$. Då hade sambandet kunnat skrivas som $T=k·l$, och man hade fått en kvot $\frac{T_{dubbellängd}}{T_{längd}}=\frac{k·2l}{k·l}=2$. Eftersom du inte fick kvoten 2 (dvs att periodtiden fördubblas om pendellängden fördubblas), så är uppenbarligen inte sambandet mellan $T$ och $l$ linjärt (vilket man snabbt kan konstatera enbart genom att titta på grafen...). Du mätte istället $\frac{T_{dubbellängd}}{T_{längd}}\approx 1.4$.

Som jag visade i kommentar #7 så blir $\frac{T_{dubbellängd}}{T_{längd}}=2^a$ ifall man ansätter sambandet $T=k·l^a$.

$2^a\approx 1.4 \Rightarrow a\approx 0.5$

Dvs med din framräknade kvot på 1.4, så blir sambandet $T=k·l^{0.5}=k·\sqrt{l}$. Vilket är precis det samband som står i din formelsamling.  

Hänger du med nu?

JohanF skrev:

Fysik321 skrev:

Visa föregående citat

JohanF skrev:

Jag tror du redan vet vilket sambandet är, dvs $T=k·\sqrt{l}$, eftersom den finns med i formelsamlingen 

Jag tror såhär om labben, om man inte först tjuvkikar i formelsamlingen, utan istället antar att du inte har en aning om sambandet före du genomför labben.

1. Du mäter, och ritar din graf över olika $T$ för olika $l$.

2. Du observerar i grafen att det ser ut att finnas något slags matematisk samband mellan T och l, men du kan inte riktigt se hur sambandet är.

3. Du resonerar vidare. Kanske sambandet kanske skrivas $T=k·l^a$, men du vet fortfarande inte värdet på exponenten $a$.

4. Värdet på exponenten $a$ kan undersökas med de kvoter som du räknat ut

$kvot=\frac{T_{dubbel}}{T}=\frac{k·{\left(2l\right)}^a}{k·l^a}=\frac{2^a{l}^a}{l^a}=2^a$

Medelvärdet på dina kvoter ser ut att bli ungefär 1.4 (du ser ut att ha räknat lite fel när du räknade ut medelvärdet på kvoterna). Vad får du alltså för värde på exponenten $a$?

Tack så jätte mycket för att du svarade på min fråga!

Jag prövade de stegen du skrev upp och jag tog ett exempel utifrån kvoten: 

 

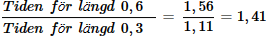
Om jag räknade rätt då fick jag det till 4.

 

Har jag förstått det rätt?

Jag prövade att räkna om medelvärdet och jag fick till det till 1,402 som du sa 1,4. Jag hade adderat det fel på miniräknaren. 

Jag tror det är nån detalj som fortfarande är oklar för dig, vi får bena i det lite till. Såhär:

Antag att $T$ hade varit proportionell mot $l$. Då hade sambandet kunnat skrivas som $T=k·l$, och man hade fått en kvot $\frac{T_{dubbellängd}}{T_{längd}}=\frac{k·2l}{k·l}=2$. Eftersom du inte fick kvoten 2 (dvs att periodtiden fördubblas om pendellängden fördubblas), så är uppenbarligen inte sambandet mellan $T$ och $l$ linjärt (vilket man snabbt kan konstatera enbart genom att titta på grafen...). Du mätte istället $\frac{T_{dubbellängd}}{T_{längd}}\approx 1.4$.

Som jag visade i kommentar #7 så blir $\frac{T_{dubbellängd}}{T_{längd}}=2^a$ ifall man ansätter sambandet $T=k·l^a$.

$2^a\approx 1.4 \Rightarrow a\approx 0.5$

Dvs med din framräknade kvot på 1.4, så blir sambandet $T=k·l^{0.5}=k·\sqrt{l}$. Vilket är precis det samband som står i din formelsamling.  

Hänger du med nu?

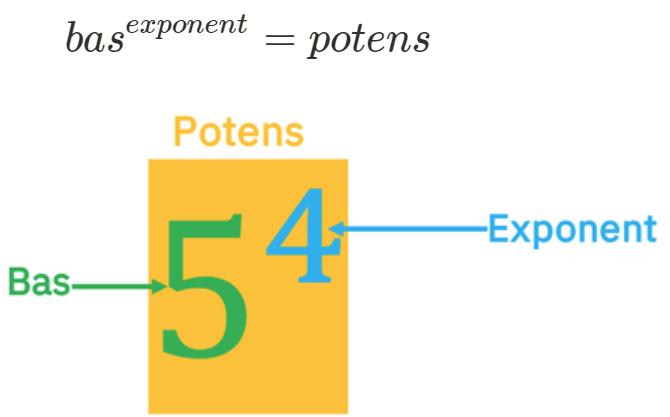
Ja! Nu börjar jag förstå bättre. Däremot den sista delen om exponent, där basen med upphöjt till a förstår jag inte lika mycket...

Vad beskriver a? 

Förlåt jag tänker väldigt långsamt och har svårigheter med svenska sammanhang och språket. 

Jag tycker du gör det jättebra. Säg till om jag använder för svår svenska!

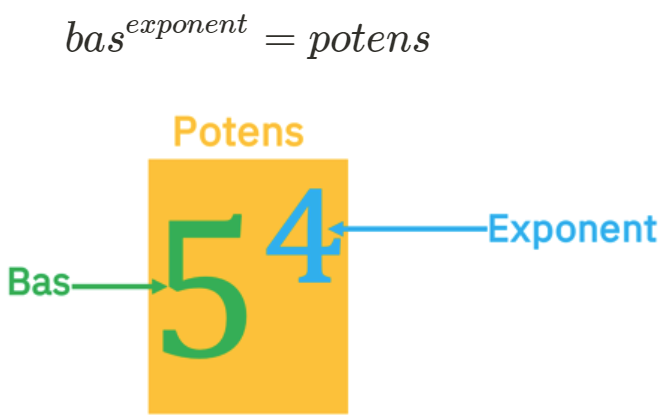
$a$ i formeln $T=k·l^a$ beskriver hur sambandet mellan svängningstiden och pendelns längd ser ut.

Antag att sambandet hade varit $a=1$, dvs $T=k·l$, då hade du fått en rak linje i din graf. Och du hade fått kvoten $\frac{T_{dubbel}}{T}=2$

Antag att sambandet hade varit $a=2$, dvs $T=k·l^2$, då hade du fått en stigande kurva i din graf. Och du hade fått kvoten $\frac{T_{dubbel}}{T}=4$

Antag att sambandet hade varit $a=-1$, dvs $T=k·\frac{1}{l}$, då hade du fått en sjunkande kurva i din graf. Och du hade fått kvoten $\frac{T_{dubbel}}{T}=0.5$

JohanF skrev:

Jag tycker du gör det jättebra. Säg till om jag använder för svår svenska!

$a$ i formeln $T=k·l^a$ beskriver hur sambandet mellan svängningstiden och pendelns längd ser ut.

Antag att sambandet hade varit $a=1$, dvs $T=k·l$, då hade du fått en rak linje i din graf. Och du hade fått kvoten $\frac{T_{dubbel}}{T}=2$

Antag att sambandet hade varit $a=2$, dvs $T=k·l^2$, då hade du fått en stigande kurva i din graf. Och du hade fått kvoten $\frac{T_{dubbel}}{T}=4$

Antag att sambandet hade varit $a=-1$, dvs $T=k·\frac{1}{l}$, då hade du fått en sjunkande kurva i din graf. Och du hade fått kvoten $\frac{T_{dubbel}}{T}=0.5$

Okej! Nu börjar jag förstå mycket bättre. Tack så jätte mycket för all din hjälp hittills