Hur påverkar tyngdaccelerationen fjädersystemet?

Det kanske hjälper med illustrationen i mitt svar här:

https://www.pluggakuten.se/trad/harmonisk-pendelrorelse-resulterande-kraft/?order=all#post-04844664-a2ce-4ef8-a74b-abad00cbe961

Ditt fel är att du frikopplar gravitationsacceleration och resulterande accelerationen som om de är oberoende. Fullständig friläggning av partikeln och Newtons andra lag kommer enkelt ge dig svar. Gör det och visa ditt försök så blir det lättare att diskutera om du har frågor.

Tack, det var till hjälp! Just att fjäderkraften aldrig byter riktning hade jag inte tänkt på innan! Det jag egentligen menade med min dumt formulerade fråga var hur man kan räkna som om gravitationen inte fanns. Jag har ett försök nedan:

Antag att vi har ett tvådimensionellt koordinatsystem där uppåt och höger är positiva riktningar, låt $\vec{g}:=\vec{(0,-g)}$ och antag att fjädern innan någon vikt hängs i har sin nedersta del i origo. Om vi hänger i en massa $m$ i fjädern kommer den förflyttas $\vec{\Delta l}$ vertikalt, tills dess att fjäderkraften är lika stor som tyngdkraften:

$\displaystyle k\vec{\Delta l}=m\vec{g}\iff \vec{\Delta l}=\frac{m\vec{g}}{k}\iff \vec{\Delta l}=\binom{0}{(-mg)/k}$

Om vi skulle dra ytterligare i vikten så orsakar vi en förflyttning $\vec{l'}$. Om vi frilägger vikten erhåller vi då:

$\displaystyle \sum_{}^{}F=F_{g}+F_{f}=\binom{0}{-mg}+\binom{0}{k(\Delta l+l')}=\binom{0}{-mg}+\binom{0}{kl'-mg}=\binom{0}{kl'-2mg}$

Uppenbarligen gör jag ju något fel här. Det som borde hända är att "mg:na" tar ut varandra, men av någon anledning blir det inte så. 

naytte skrev:

Tack, det var till hjälp! Just att fjäderkraften aldrig byter riktning hade jag inte tänkt på innan!

Notera väl att det gäller bara om du drar ned massan kortare än avståndet till osträckt läge för fjädern. 

Det jag egentligen menade med min dumt formulerade fråga var hur man kan räkna som om gravitationen inte fanns. 

Matematiskt är det för att stationära kraften i fjädern och tyngdkraften tar ut varandra. Därmed bidrar inte tyngdkraften till resulterande accelerationen. Konceptuellt är det för att förändringen av total mekanisk energi med avseende på tid inte beror på gravitationen. Du kan härleda rörelseekvationerna genom att derivera total energi med avseende på tid. 

Antag att vi har ett tvådimensionellt koordinatsystem där uppåt och höger är positiva riktningar, låt $\vec{g}:=\vec{(0,-g)}$ och antag att fjädern innan någon vikt hängs i har sin nedersta del i origo. Om vi hänger i en massa $m$ i fjädern kommer den förflyttas $\vec{\Delta l}$ vertikalt, tills dess att fjäderkraften är lika stor som tyngdkraften:

$\displaystyle k\vec{\Delta l}=m\vec{g}\iff \vec{\Delta l}=\frac{m\vec{g}}{k}\iff \vec{\Delta l}=\binom{0}{(-mg)/k}$

Begrunda det fetmarkerade ovan och fundera sedan en gång på riktningen du fått fram för $\vec{\Delta l}$. Betänk speciellt att det vid jämvikt gäller att:

$\displaystyle \sum \vec{F} = 0$

Tillägg: 22 apr 2024 16:31

Glömde bort att det kanske är okänt för dig men allmänt gäller för en fjäder att:

$\vec{F} = - k\cdot \vec{x}$ 

För någon endimensionell förskjutningsvektor $\vec{x}$. Detta för att kraften enligt hookes lag motverkar förskjutningen och är motriktad.

Begrunda det fetmarkerade ovan och fundera sedan en gång på riktningen du fått fram för $\vec{\Delta l}$.

Jag valde riktningarna så som kändes naturligt, spelar det någon roll hur man definierar riktningarna? Om man räknar med ett minustecken framför fjäderkonstanten hamnar man väl ändå i situationen jag hamnade i?:

$\displaystyle -k\vec{\Delta l}+m\vec{g}=0 \iff k\vec{\Delta l}=m\vec{g}$

Jag ser inte heller något fel med riktningen. Om uppåt är positiv riktning kommer förskjutningen och förskjutningen är nedåt, ska y-koordinaten vara negativ. Det blir den ju också eftersom g är en positiv konstant och koordinaten blir $-mg/k$. Jag är nog fast i något sorts feltänk här. Vad exakt är det som blir fel där?

Ja, men du har $\vec{\Delta l} = (0,-\Delta l)$ och $\vec{g} = (0,-g)$ så du får:

$-k(0,-\Delta l)+ m(0,-g)=0$

$\Delta l = mg/k$

Detta vet du också redan att resultatet är direkt från en friläggning med kraftjämvikt. Du sjabblade egentligen bara till matematiken på grund av att du tappade riktningen på krafterna under vägs.

Nyckeln här är just Hookes lag. Vilket du kommer se när du gör den sista kraftsumman igen, alltså:

$\displaystyle \sum \vec{F} =\vec{F}_g+\vec{F}_f$

Jag tänkte att $\Delta l$ var ett negativt tal redan, dvs. att teckeninformationen fanns i det algebraiska objektet. Jag antar att det som blir fel där är att jag låter teckeninformationen ligga i variabeln för $\vec{\Delta l}$, medan jag skriver ut den explicit för tyngdaccelerationens koordinat?

Och nu när jag räknar med den revideringen får jag:

$\Delta l=\frac{mg}{k}\implies \sum_{}^{}\vec{F}$

$=\vec{F}_f+\vec{F}_g=-k(0,-(\Delta l+l'))+(0,-mg)=(0,mg+kl'-mg)=(0,kl')=-k\vec{l'}$

Och det verkar stämma! Har jag räknat rätt här?

Japp, jag tycker allt ser bra ut.

Om vi går tillbaka till ditt ursprungliga inlägg ser allt bra ut om du istället använder Hookes lag på sin korrekta form. Det var egentligen det enda felet.

Det jag menade med "fundera på riktningen" i detta inlägg var att fundera på vilken riktning kraften i fjädern får pga $\Delta l$, och hur du visar detta på vektorform. Egentligen försökte jag väl hinta till Hookes lag, på ett ganska klumpigt sätt.

Ah, och nu när jag tittar igenom mitt första försök igen ser jag felet, tror jag. Visst ska det vara $-k$ här:

Är det det du menar med den "korrekta formen" på Hookes lag?

Aaa, nu förstår jag, du tänker att förspänningslängden $l^\prime$ också ska ha ett negativt värde?

$l^\prime =-\frac{mg}{k}$ vid jämvikt ($\Delta l = 0$).

Alltså borde du i sumnan få $-k(\Delta l+l^\prime)-mg=-k\Delta l +k\frac{mg}{k}-mg = -k\Delta l$

Edit: Förstod inte beteckningarna, tycker fortfarande du ska göra en skiss med beteckningarna införda :)

Japp, exakt! (men jag tänkte tvärtom, alltså att $\Delta l = -mg/k$, dvs. att $\Delta l$ var storleken på utsträckningen pga att vikten bara hänger och att $l'$ var den ytterligare utsträckning vi skapar genom att dra i vikten). Men ja, exakt! Lägger in en bild imorgon!

Det verkar ha blivit lite snurrigt märker jag, ser ut att vara mitt fel.

Tänk på att variabeln $l'$ i detta fall bär tecken, och byter tecken när den passerar origo vid jämviktsläge. Detta därför att du lagt den utefter en axel i den matematiska beskrivningen. 

Du har fått resultatet nedan:

Jämför nu detta med vad du förväntar dig att få. Resulterande kraft bör vara riktad uppåt vid nedersta läge då $l'<0$. För det till vänster ovan blir det inte så och sedan rättar du magiskt till det med vektorn till höger.

Det som trixar till det för dig är här:

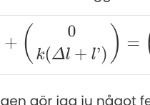
Där bör det stå:

$-k(-\Delta l+l')$

Förskjutningen vid statisk jämvikt $\Delta l$ får sitt tecken relativt ospänt läge. Du har ju effektivt gjort en variabelsubstitution från en ursprunglig koordinat $l$ med origo vid ospänt, obelastat läge för fjädern. Alltså att:

$l'=l+\Delta l$

Där det för fjädern från ospänt läge till slutliga vi diskuterat gäller att:

$\vec{F}_f=(0,-k(l))=(0,-k(-\Delta l+l'))$

Jag hoppas det klarnar nu och jag får ursäkta. 

Tillägg: 23 apr 2024 01:36

Å andra sidan, om jag också missförstått dina variabler och beteckningar väntar jag ivrigt på en bild.

Här kommer bilden:

I läget längst till vänster hänger ingenting i fjädern. Sedan hängs det i en vikt med massa $m$ som sträcker ut fjädern lite tills dess att fjäderkraften är lika stor som tyngdkraften. I det högra läget har man dragit ned vikten ytterligare med en förskjutning $\vec{l'}$, dvs. om man släpper kommer den börja svänga harmoniskt. Vi definierar:

$\vec{g}:=(0,-g)$, $\vec{\Delta l}:=(0,\Delta l)$ och $\vec{l'}:=(0,l')$. 

Om vi frilägger vikten i det högra läget och analyserar krafterna ser vi att:

$\displaystyle \sum_{}^{}\vec{F}=\vec{F_f}+\vec{F_g}$

Fjäderkraften som verkar kommer verka för summan av de två förskjutningsvektorerna $\vec{\Delta l}$ och $\vec{l'}$. Det betyder att:

$\displaystyle \vec{F_f}+\vec{F_g}=(0,-k(\Delta l+l'))+(0,-mg)$

Vi vet dessutom från det mittersta läget att $\vec{\Delta l}=-m\vec{g}/k$. Om vi multiplicerar in $-k$ erhåller vi:

$\displaystyle \vec{F_f}+\vec{F_g}=(0,mg-kl')+(0,-mg)=(0,mg-mg-kl')=-k(0,l')$

Det som vi har kommit fram till nu är att gravitationskraften som verkar på vikten inte påverkar den harmoniska svängningsrörelsen, om man räknar med punkten $(0, \Delta l)$ som jämviktsläge (fjäderns nedre del låg i origo från början). 

Ser det rätt ut? Här tänker jag att både $\Delta l$ och $l'$ innehåller själva teckeninformationen, dvs. man behöver inte bry sig om huruvida det är negativt eller positivt tecken. Det gör det också mer allmänt, eller hur? Man hade väl kunnat använda samma resonemang på en ihoptryckning av fjädern istället för en förlängning?

OBS: Det här är typiskt en sådan sak som jag tycker är bättre att ta när man kan rita och ställa upp ordentligt. Se nedan diskussion som akademiskt kåseri, snarare än någon slags strikt rekommendation.

Redundant teckeninformation

Jag skulle nog bara säga att teckeninformationen i $\Delta l$ är redundant för att den bestäms implicit när du satt ditt ursprungliga origo vid ospänt läge. Sedan blir det också så att du redan bestämt ett koordinatsystem och därmed är det givet att vektorn $\vec{\Delta l}$ är negativ, med storlek $\Delta l=mg/k$.

Konsekvens

Utan detta, när du ska föra in siffror istället för $\Delta l$, kommer du behöva referera till ursprungligt origo. Samtidigt, i samma uttryck, ska du då referera till det nya origo du definierat vid jämviktsläge när du beskrev $l'$. Detta är bäddat för att det lätt kan bli fel. 

Resolution

Om du istället betraktar det som ett variabelbyte så blir $\Delta l$ snarare en konstant med ett positivt värde av storlek $mg/k$. Men, som du hintar till, kan det lika gärna vara en konstant med negativt värde som du adderar till $l'$ så att $l=-\Delta l$ om $l'=0$.

Vad är mest allmänt?

Huruvida det är mer allmänt på det ena eller andra sättet ser jag inget stöd för riktigt. Elongationen av fjädern är alltid i samma riktning som tyngdkraften, oberoende av tecken på $l'$. Alltså är inte $\Delta l$ en variabel som kan byta tecken för detta problem.

Jag skulle nog bara säga att teckeninformationen i $\Delta l$ är redundant för att den bestäms implicit när du satt ditt ursprungliga origo vid ospänt läge. Sedan blir det också så att du redan bestämt ett koordinatsystem och därmed är det givet att vektorn $\vec{\Delta l}$ är negativ, med storlek $\Delta l=mg/k$.

Jo, det har du rätt i faktiskt. Fjädern kommer ju inte tryckas ihop då man hänger i vikten!

Alltså är inte $\Delta l$ en variabel som kan byta tecken för detta problem.

Nej, precis. Det är ju $l'$ som kan byta tecken beroende på om man trycker ihop fjädern eller drar ut den.

Men ser det rätt (om än otympligt) ut nu i mina beräkningar när bilden finns till hands?