partikulär lösning sin

Jag har fått homogena lösningen $y_{h} (t) = A \cos (t) + B \sin (t)$ , då det borde vara lösningen till svängnings ekvationen. Jag ansätter sedan $y_{p} (t) = a \cos (t) + b \sin (t)$ som partikulär lösning för att försöka hitta a och b. När jag sedan räknar det och sätter det lika sin(t) får jag dock att 0 = sin(t). Hur ska man tänka här?

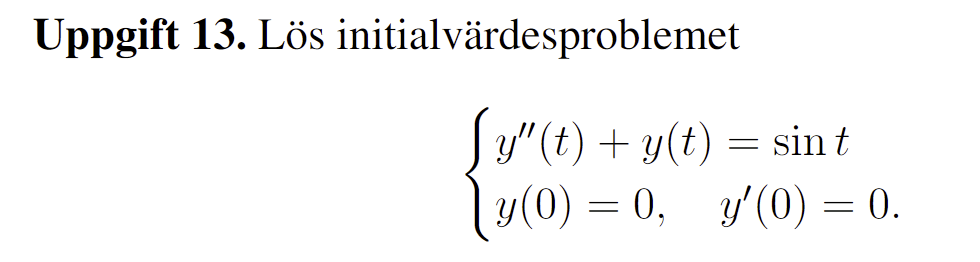
Problemet med din gissning $y_p$ är att den löser den homogena ekvationen. När det inträffar är standardtipset att multiplicera med $t$ så många gånger som behövs.

Testa alltså ansatsen $y_p=tA\cos(t)+tB\sin(t)$

Visa spoiler

y_p=-\frac12 t \cos(t)

Det visste jag inte, tack!

Svara