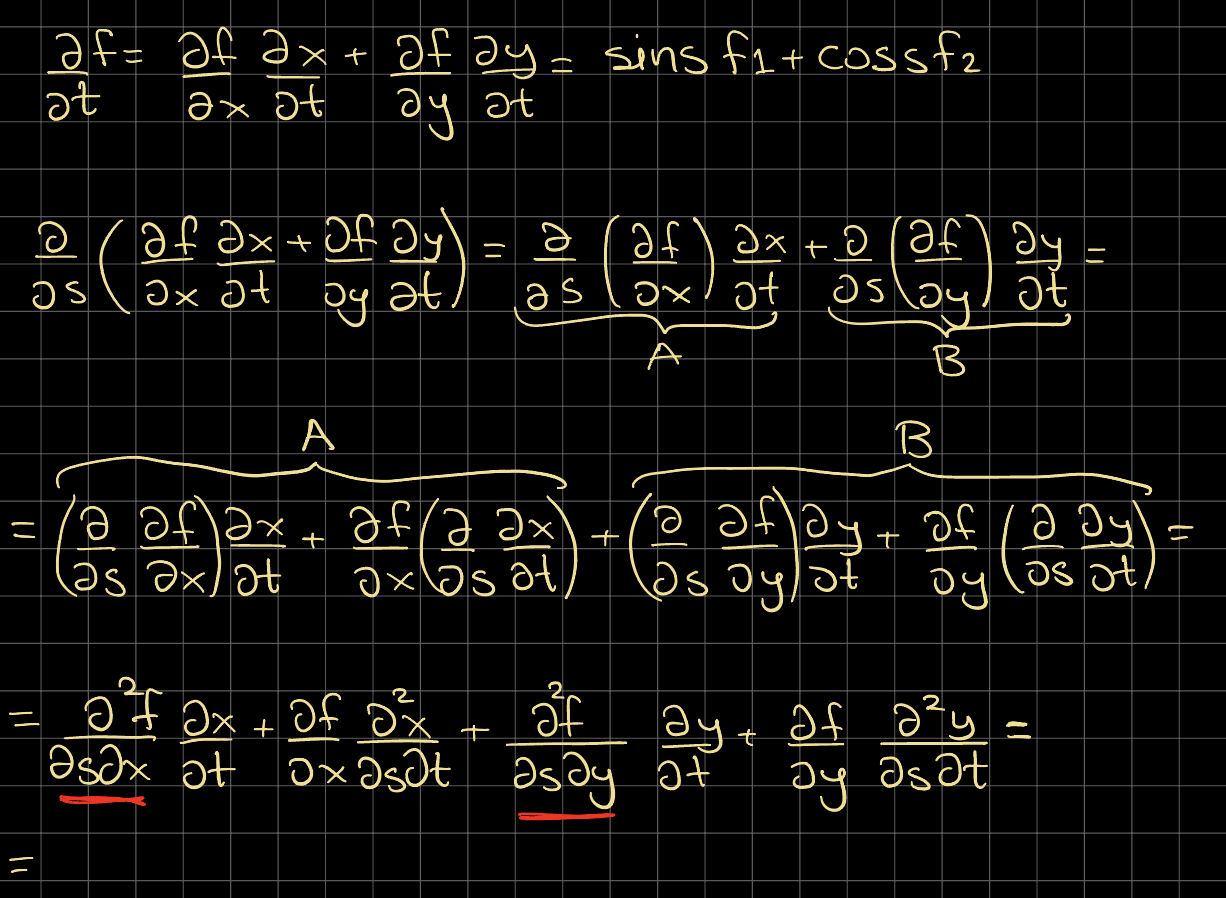Detta är inte lätt tycker jag.
Men efter första likhetstecknet har de bara deriverat med avseende på t, det är först i andraderivatan som de deriverar m a på s.
Nu tror jag att jag hittat ett sätt att komma åt detta. Det blir överskådligare för mig om jag väljer ett exempel.
Låt f(x, y) = x4 y7 . Vi har redan x = t sin s och y = t cos s
Då fås df/dt = df/dx dx/dt + df/dy dy/dt =
= 4x3 y7 sin s + x4 7y6 cos s
Detta ska deriveras med avseende på s. Jag bryr mig bara om första termen här, den andra behandlas analogt.
d/ds ( 4x3y7 sins) = 4x3y7 cos s + [12x2 y7 tcos s + 4x3 7y6 (–tsin s)] sin s
Alltså, d/ds ( 4x3 y7 sins) = f1 * d/ds(dx/dt) + [f11 dx/ds + f12 dy/ds ] * dx/dt
eller
f1 cos s + f11 t cos s sin s – f12 t sin s sin s
Nu kan andra termen df/dy * dy/dt deriveras med avseende på s efter samma mönster.
För mig underlättade det att ha x4 y7 som exempel. Men man behöver göra det själv för att se hur det funkar.
d/ds ( 4x3y7 sins) = 4x3y7 cos s + [12x2 y7 tcos s + 4x3 7y6 (–tsin s)] sin s
Förstår att x och y är funktioner av s. Du har inte inkluderat ett antal mellansteg antar jag?
Ja x = t sin s , y = t cos s
x och y är funktioner av s och t.
Inkluderat mellansteg, vet inte riktigt vad du menar.
Tänk på att derivatan av en produkt är
Här har du en produkt av två funktioner

Den sista termen ger också en derivata:
D4NIEL skrev:
Tänk på att derivatan av en produkt är
Här har du en produkt av två funktioner

Den sista termen ger också en derivata:
Tänkte inte på att x beror på s. Ska försöka lösa på nytt när jag har möjligheten. Tack ska du ha.
D4NIEL skrev:
Tänk på att derivatan av en produkt är
Här har du en produkt av två funktioner

Den sista termen ger också en derivata:
Har gjort ett nytt försök nu, hur ska jag tolka det markerat i rött(i den nya bilden)?
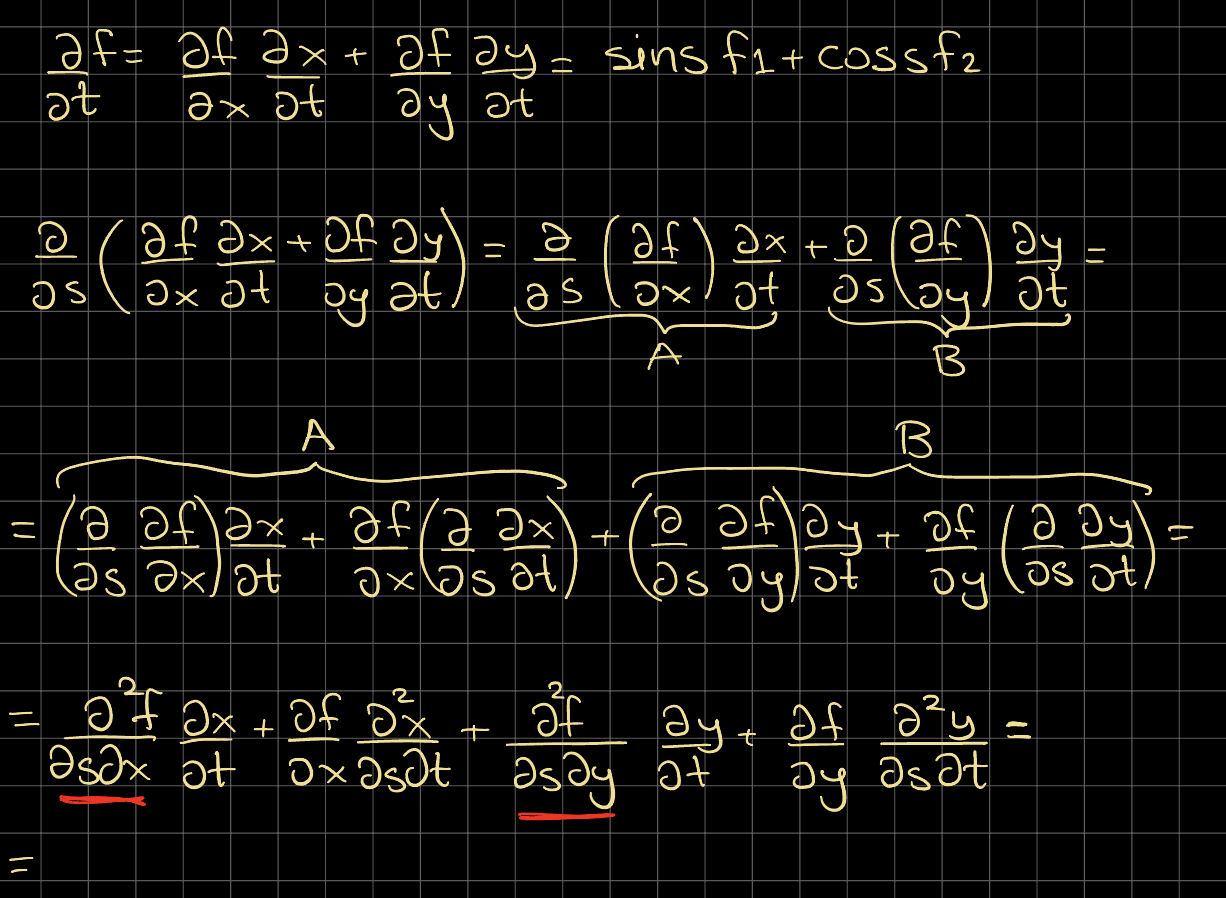
beror av samt
Man kan ibland lite slarvigt skriva osv
D4NIEL skrev:
beror av samt
Förstår inte hur du får högerledet
Det är bara kedjeregeln, kanske blir det lättare om vi kallar något annat, t.ex.
D4NIEL skrev:
Det är bara kedjeregeln, kanske blir det lättare om vi kallar något annat, t.ex.
Tack ska du ha, känner att det sitter nu :)