Partiell integration

Hej!

Har lite svårt att se vad som blir fel i följande beräkning där jag ska utveckla integralen $\int x \times \cos (x)$ med partiell integration. Har testat utveckla genom att låta U=cos(x) samt dV=x, och tvärtom men får inte ut det rätta svaret.

Lösning:

Låter $U = x$ , då är $d U = 1 \times d x$ .

Låter $d V = \cos (x)$ , då är $V = \sin (x)$ .

Sedan använder jag $\int U \times d V = U \times V - \int V \times d U$ , (från boken) och det jag gör i princip är att jag ersätter varje variabel med de jag bestämde här ovan (det är iallafall så jag tänker att man ska göra???). Så får då:

$\int x \times \cos (x) = x \times \sin (x) - \int \sin (x) \times 1 \times d x$ , där jag förenklar höger led till att bli,

$x + C$ , eftersom sin(x) tar ut varandra? Känner själv att det blir fel någonstans, men kan inte komma på var. Någon som kan hjälpa/ge någon ledtråd? Rätta svaret är $x \times \sin (x) + \cos (x) + C$

Så här ser partiell integration ut

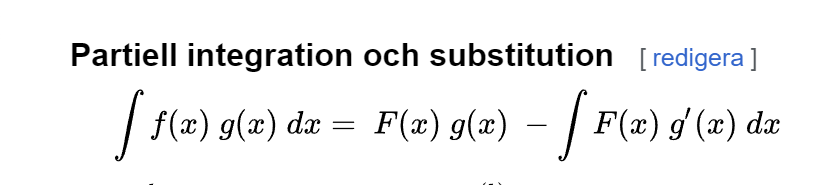
Du ska alltså hitta en primitiv till din ena funktion och derivera den andra

I ditt fall låter jag f(x) vara cos(x) och x vara g(x)

$\int x * \cos (x) d x = x * \sin (x) - \int 1 * \sin (x) d x = x * \sin (x) + \cos (x) + C$

Är det för att du flyttar över $\int$ $- 1 * \sin (x) d x$ till vänster ledet? Så det står egentligen:

$x * \cos (x) + \sin (x) * 1 + C = \sin (x) * x$ ?

Jag kanske gick lite snabbt fram,

x*cos(x) ska vi integrera

f(x) = cos(x) => F(x) = sin(x)
g(x) = x => g'(x) = 1

steg 1 i vår integrering

$\int f (x) * g (x) d x = F (x) * g (x) - \int g' (x) * F (x) d x$

med våra funktioner:

$\int \cos (x) * x d x = \sin (x) * x - \int \sin (x) * 1 d x$

då har vi fått dels x*sin(x) samt en ny integral, som vi i nästa steg ska hitta en primitiv till, det ser vi direkt att det blir -cos(x)

Alltså får vi i steg 2

$\int x * \cos (x) d x = x * \sin (x) + \cos (x) + C$

Som är vår lösning.

Svara

Visa senaste svar