Partiell derivata 2
Hej, har uttryckt andraderivatan med Leibniznotation, är den korrekt? Facit uttrycker lösningen annorlunda. Om min lösning är korrekt, hur ska man tänka när man ska skriva om som facit gör? vad blir exempelvis i funktionsuttryck?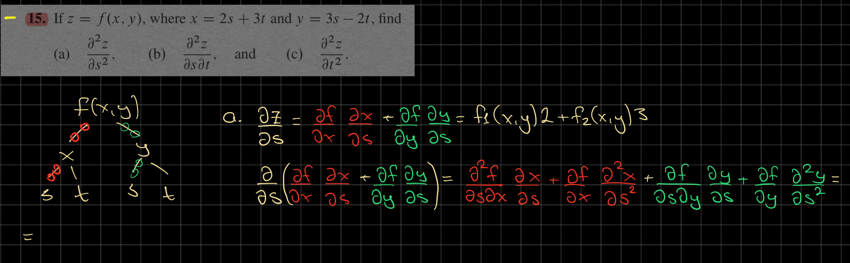
Facit
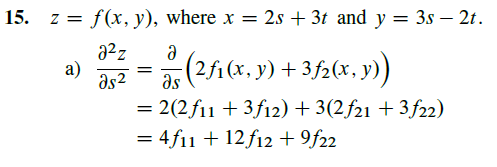
Första derivatan är rätt. Sen när du ska derivera med s igen borde du använda uttrycket som står längst till höger på översta raden, och inte det till vänster. Sedan när du deriverar df/dx med s så får du (d^2f/dx^2)(dx/ds)=2f11
Calle_K skrev:Första derivatan är rätt. Sen när du ska derivera med s igen borde du använda uttrycket som står längst till höger på översta raden, och inte det till vänster. Sedan när du deriverar df/dx med s så får du (d^2f/dx^2)(dx/ds)=2f11
Kalla mig galen men är inte denna videon en mer konsekvent eller logisk förklaring till hur man gör? https://www.youtube.com/watch?v=7YbbWIxpPIk&t=183s&ab_channel=Yev%27sNotes
Det är i och för sig väldigt mycket arbete, men hur annars ska man få de uttrycken?
Skulle säga att det där är en mer generell approach. Kommer funka i alla lägen för alla funktioner. Så absolut en bra metod att kunna använda sig av.
I detta fall kommer B (=dx/ds) vara en konstant och därmed får vi bara den första termen. Vidare kommer d/ds(df/dx) vara d^2f/dx^2*(dx/ds)+d^2f/dydx*(dy/ds) (Ser nu också att jag skrev fel i min första kommentar).


