Parallelltrapets med arean 1 a.e
Jag har försökt lösa uppgift 13 b) och behöver hjälp.

Jag förstår inte hur jag ska gå tillväga för att hitta punkten Q om jag inte vet vilken punkt på grafen jag ska derivera för att hitta tangenten.
All hjälp uppskattas!
Jag kunde inte lägga in båda bilderna så här är första delen av uppgiften:

Kan du redigera de båda bilderna så att det går att läsa dem?
Smaragdalena skrev:Kan du redigera de båda bilderna så att det går att läsa dem?
Så, hoppas det går att läsa nu :)
Ja, nu går det att läsa.
Förslag på a-uppgiften: Börja med att sätta upp formeln för arean av ett parallelltrapets så att du vet vilka obekanta storheter du behöver bestämma.
Yngve skrev:Ja, nu går det att läsa.
Förslag på a-uppgiften: Börja med att sätta upp formeln för arean av ett parallelltrapets så att du vet vilka obekanta storheter du behöver bestämma.
Tack, lyckades lösa a) uppgiften. Kan jag få hjälp med b), det skulle uppskattas starkt? :)
Låt Q ha koordinaterna (x, 1/x2).
Sött upp ett uttryck för tangentens ekvation, då ser du var den skär y-axeln.
Använd sedan formeln för arean av ett parallelltrapets för att sätta upp en ekvation där du kan lösa ut x
Yngve skrev:Låt Q ha koordinaterna (x, 1/x2).
Sött upp ett uttryck för tangentens ekvation, då ser du var den skär y-axeln.
Använd sedan formeln för arean av ett parallelltrapets för att sätta upp en ekvation där du kan lösa ut x
Tangentens ekvation, blir det derivatan d.v.s -2*1/x³?
Hur ska jag använda det i formeln för arean?
Tangentens ekvation, blir det derivatan d.v.s -2*1/x³?
Hur ska jag använda det i formeln för arean?
Du vet att tangenten har lutningen -2/x3 och går genom punkten (x,1/x2). Skriv tangentens ekvation på formen y = kx+m (k vet du ju redan), så får du skärningen med y-axeln. Kommer du vidare härifrån?
Smaragdalena skrev:Tangentens ekvation, blir det derivatan d.v.s -2*1/x³?
Hur ska jag använda det i formeln för arean?
Du vet att tangenten har lutningen -2/x3 och går genom punkten (x,1/x2). Skriv tangentens ekvation på formen y = kx+m (k vet du ju redan), så får du skärningen med y-axeln. Kommer du vidare härifrån?
Jag fick m=3/x² men då blir hela tangentens ekvation exakt samma som f(x) d.v.s 1/x².
Det verkar mysko. Visa steg för steg hur du fick fram det, så kan vi hjälpa dig vidare.
Smaragdalena skrev:Det verkar mysko. Visa steg för steg hur du fick fram det, så kan vi hjälpa dig vidare.
Detta är hur jag gjorde, jag kan vara helt ute och cyklar
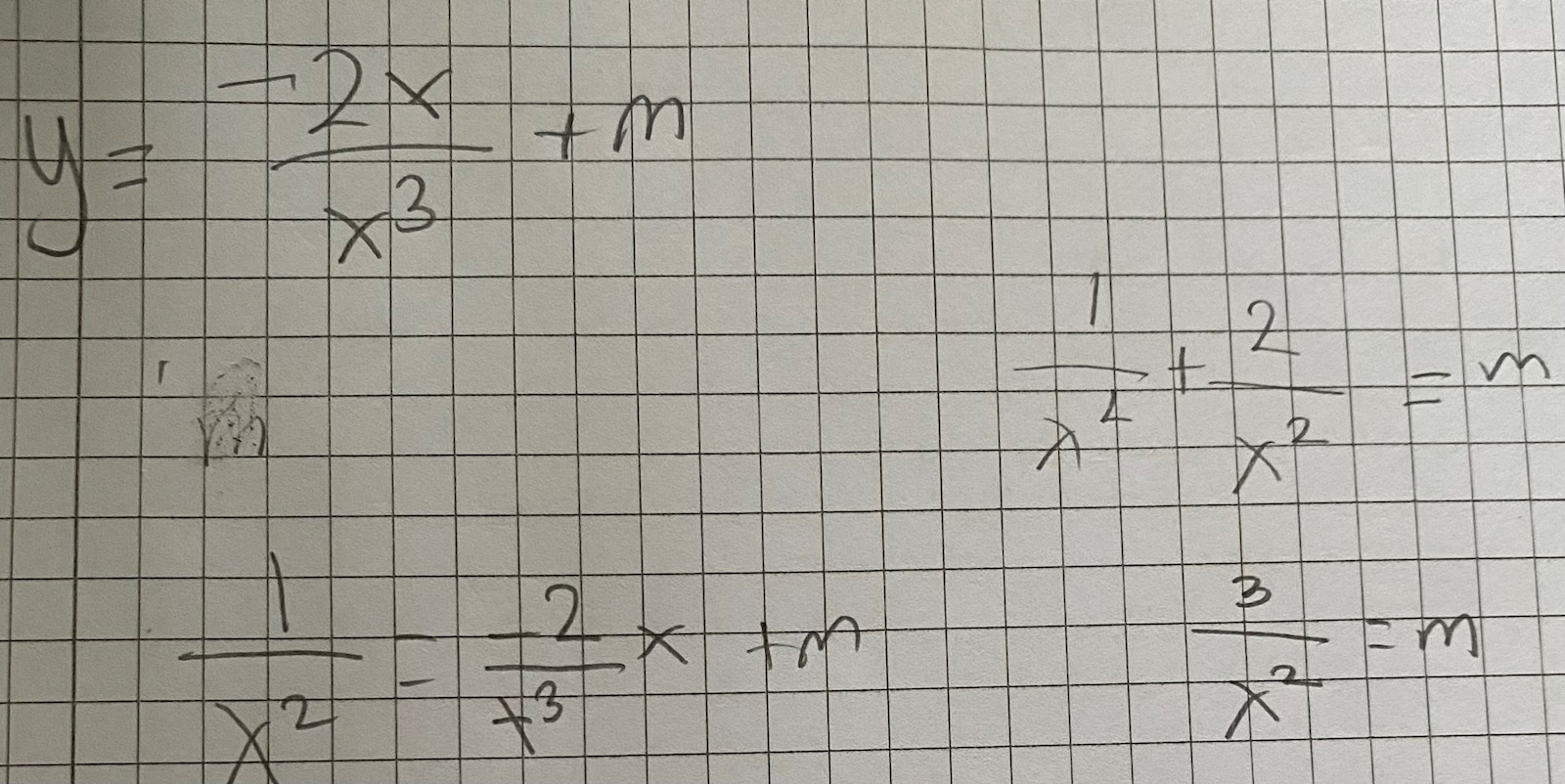
Det är mitt fel att det blev rörigt med vilket x som är vilket.
Jag borde ha sagt att x-koordinaten för punkten Q är t.ex. .
Då blir koordinaterna , tangentens lutning och tangentens ekvation då .
Med den kända punkten på tangenten får vi , vilket ger oss
Tangentens ekvation är alltså .
Kommer du vidare därifrån?
Yngve skrev:Det är mitt fel att det blev rörigt med vilket x som är vilket.
Jag borde ha sagt att x-koordinaten för punkten Q är t.ex. .
Då blir koordinaterna , tangentens lutning och tangentens ekvation då .
Med den kända punkten på tangenten får vi , vilket ger oss
Tangentens ekvation är alltså .
Kommer du vidare därifrån?
Jag har en fråga, hur ska jag använda formeln för arean? Jag antar att h är tangentens ekvation men a och b förvirrar mig.. (i formeln h(a+b)/2)
Mimiii542 skrev:
Jag har en fråga, hur ska jag använda formeln för arean? Jag antar att h är tangentens ekvation men a och b förvirrar mig.. (i formeln h(a+b)/2)
Nej, h är avståndet mellan de två parallella sidorna. a och b är längderna av de två andra sidorna.
Se här.
Yngve skrev:Mimiii542 skrev:Jag har en fråga, hur ska jag använda formeln för arean? Jag antar att h är tangentens ekvation men a och b förvirrar mig.. (i formeln h(a+b)/2)
Nej, h är avståndet mellan de två parallella sidorna. a och b är längderna av de två andra sidorna.
Se här.
Jaha, kan jag inte använda integraler för att beräkna arean?
Jo, men det är enklare att använda areaformeln för parallelltrapets eftersom du känner till alla mått.
Okej så höjden blir 3/a² och en av parallellerna är 1/a², vad är den sista parallellen då?
Menar att uttrycket blir (3/a²(b+1/a²))/2
Mimiii542 skrev:Okej så höjden blir 3/a²
Nej, h är avståndet mellan de två parallella sidorna. Jag har markerat det i bilden.
Jag har även rödmarkerat de två sidorna som har olika längder (a och b i formeln).

Yngve skrev:Mimiii542 skrev:Okej så höjden blir 3/a²
Nej, h är avståndet mellan de två parallella sidorna. Jag har markerat det i bilden.
Jag har även rödmarkerat de två sidorna som har olika längder (a och b i formeln).
Tack så jättemycket, jag förstod äntligen!



