På hur många sätt kan man skapa ett femsiffrigt nummer av 7 siffror?
Du får använda talen 2-8, hur många 5-siffriga telefonnummer kan du skapa om:
a) siffrorna INTE får upprepa sig och måste komma i ökande ordning. Exempelvis är 23478 okej men 32678 inte okej.
b) siffrorna får upprepa sig, men måste komma i ökande ordning. exempelvis är 24448 okej men 24484 inte okej.
På a) tänkte jag att antalet sätt borde bli:
eftersom det endast finns ett sätt att storleksordna en kombination. Antal kombinationer borde således motsvara antalet sätt att skapa numret på, eftersom varje kombination "hör ihop" med en storleksordning.
På b) blev det lite klurigare men jag tror att jag fick till det. Om man utvidgar mängden med element man väljer ur så att den inkluderar varje siffra 5 gånger finns det totalt 7 · 5 = 35 olika element. Samma resonemang gäller här, att om man väljer ut 5 godtyckliga element av dessa 35 element kommer varje kombination höra ihop med en storleksordning. Det finns inget sätt att välja fem av dessa som gör att man inte kan storleksordna dem på exakt ett sätt. Svaret på b bör således vara:
.
Verkar detta rimligt?
EDIT:
På djupare eftertanke verkar det uppstå ett problem. På b-uppgiften tror jag att jag räknar samma tal flera gånger. Eftersom varje element anses vara särskilt så kommer jag få talet 21 22 2 2 2 räknat som ett annat tal än 22 21 2 2 2. Kan man fixa detta genom att bara dela C(35, 5) på 5! ? Jag tänker att varje tal borde uppträda 5! gånger.
Du ska välja 5 element av 7.
I a har vi inte återläggning, och ordningen spelar ingen roll (låter konstigt för de måste ju ligga i ordning, men man kan se det som att 23478 är samma val som 24783).
Så där får jag 7 över 5 eller 21 möjligheter som du.
I b har vi återläggning tillåten och med samma terminologi blir det att ordningen inte spelar roll.
Här kan man tänka att man har en bräda med 7 skålar i rad, numrerade 2, 3, …, 8. Vi lägger 5 kulor i skålarna och läser av. Hamnar en kula i skål 2, tre kulor i skål 4 och en kula i skål 8, så motsvarar det numret 24448, oavsett i vilken ordning kulorna hamnade där.
Vi har alltså
| x | | xxx | | | | x |
2 3 4 5 6 7 8
Vi kan låta de lodräta strecken vara bokstaven i så har vi ”ordet” ixiixxxiiiixi. Vi vill räkna hur många sådana ord det finns.
Men stopp, alla ord kommer börja och sluta på ”i”. Så det första och sista i-et kan tas bort, de ökar inte antalet tänkbara ord.
Vi har nu ordet xiixxxiiiix. Det består av 6 ”i” och 5 ”x”, totalt 11 bokstäver. Om man mött det klassiska MISSISSIPPI – hur många ord kan bildas av bokstäverna i det ordet – så ser man att antalet nummer du söker är 11! / (6! 5!), dvs (11 över 5) = 462.
Jag postar nu och tittar om jag gjort rätt sedan.
Ett skrivfel såg jag, redigerat nu. Om någon tycker sig ana att min framställning påverkats av Grimaldis bok om diskret matematik, så kan det kanske inte är helt obefogat. Mer än tio år sedan jag hade den i min hand, men jag tror jag minns rätt.
Jag förstår inte riktigt metoden du hänvisar till. Alltså jag förstår att vi räknar med stars and bars och att du utgår från 11 element (fem siffror och 6 tuplar) och att du delar bort alla identiska tupeluppsättningar. Men varifrån kommer 5! i nämnaren?
Jag tänkte något i denna stilen:
Låt varje siffra komma i uppsättningar om fem: 21 22 23 24 25... osv. Då finns det totalt 35 siffror. Då väljer vi först ut fem av dessa 35:
Nu har vi alla sätt att välja ut siffrorna på. Sedan kör vi på "stars and bars"-approachen:
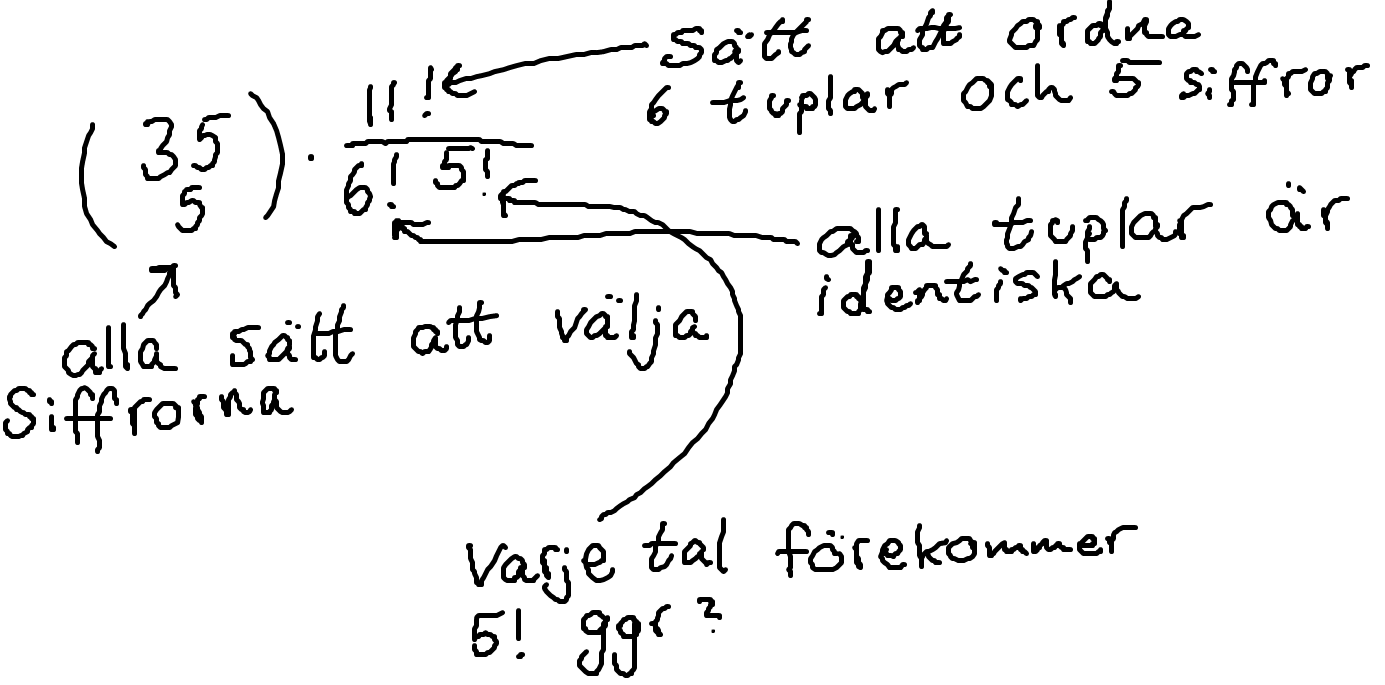
Glöm tanken jag postade ovan, den är helt efterbliven. Men jag har en ny tanke.
Om man bara räknar C(35, 5) kommer samma tal uppträda flera gånger, t.ex:
21 3 4 4 4
räknas som ett annat tal än
22 3 4 4 4
Men för varje unikt tal som existerar kan man välja varje siffra på fem olika sätt (fem siffror som är likadana). Således kommer varje unikt ord räknas 5*5*5*5*5 = 55 gånger för mycket (tror jag). Låter det rimligt?


