P(avvisa partiet efter båda kontrollerna)=?
Hej! Jag försöker lösa b)-uppgiften. a)-uppgiften gick bra och jag försökte lösa b)-uppgiften på liknande sätt men får fel svar:( Har dubbelräknat men får fortfarande fel svar, vet inte riktigt vad jag gör fel?

Facit:
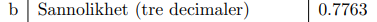
Min lösning:

Tack på förhand!
Jag är inte helt säker på att jag följer din räkning. Jag är också lite osäker på vad som menas i uppgift b. Är det att man accepterar i första kontrollen men avvisar i andra kontrollen, eller är det att man avvisar i antingen första ELLER andra kontrollen?
Spontant känns det ändå som att det är första alternativet, dvs, att man accepterar i första men avvisar i andra kontrollen.
Jag skulle räknat såhär: Låt A vara händelsen att man accepterar i första kontrollen, och B vara händelsen att man avvisar i andra kontrollen. Då vill du räkna P(A och B) = P(A) P(B|A). P(A) kan du få från a)-uppgiften (det är komplementet till vad du räknat där). P(B|A) är vad du räknat ut när du räknat 1- (50 välj 10) / (55 välj 10).
Stämmer detta tro?
Hondel skrev:Jag är inte helt säker på att jag följer din räkning. Jag är också lite osäker på vad som menas i uppgift b. Är det att man accepterar i första kontrollen men avvisar i andra kontrollen, eller är det att man avvisar i antingen första ELLER andra kontrollen?
Spontant känns det ändå som att det är första alternativet, dvs, att man accepterar i första men avvisar i andra
Jag tolkar det som andra alternativet. Annars hade väl "avvisa ett parti efter andra kontrollen" varit en bättre formulering.
Hondel skrev:Jag är inte helt säker på att jag följer din räkning. Jag är också lite osäker på vad som menas i uppgift b. Är det att man accepterar i första kontrollen men avvisar i andra kontrollen, eller är det att man avvisar i antingen första ELLER andra kontrollen?
Spontant känns det ändå som att det är första alternativet, dvs, att man accepterar i första men avvisar i andra kontrollen.
Jag skulle räknat såhär: Låt A vara händelsen att man accepterar i första kontrollen, och B vara händelsen att man avvisar i andra kontrollen. Då vill du räkna P(A och B) = P(A) P(B|A). P(A) kan du få från a)-uppgiften (det är komplementet till vad du räknat där). P(B|A) är vad du räknat ut när du räknat 1- (50 välj 10) / (55 välj 10).
Stämmer detta tro?
Jag blir också osäker på hur de menar, men tänker också att det är det första alternativet. Jag tänker att de frågar efter sannolikheten att avvisa ett parti efter båda kontrollerna. Men för att partiet ens ska komma till den andra kontrollen måste det väll accepteras i första eftersom annars, om den avvisas i första, så går den väll inte vidare till den andra kontrollen? Så jag drog slutsatsen att den måste ha accepterats i första kontrollen. Och kravet för att bli accepterad i första kontrollen var att inte någon av de 5 valda enheterna fick vara defekta. Så det borde bli så här:
Kontroll 1:
-välj 5 av 60 enheter varav där 5 är defekta och 55 är felria
-partiet accepteras av kontrollen => de 5 valda enheterna var felfria
-De 55 enheterna som inte valdes i första kontrollen går vidare till kontroll 2, i kontroll 2 har vi alltså 50 felfria (efter som 5 felfria redan kontrollerats i kontroll 1) och fortfarande 5 defekta.
Kontroll 2.
-Välj 10 av 55 enheter varav 5 är defekta och 50 är felfria.
borde man inte kunna använda gynsamma/möjliga fall som jag gjort ovan?
Tyvärr stämde inte P(A och B) då = 0,363 så vi får att P(A) =0,637
så vi får att P(A|B)*P(A) =0,6487*0,637=0,4132...:(
Calle_K skrev:Hondel skrev:Jag är inte helt säker på att jag följer din räkning. Jag är också lite osäker på vad som menas i uppgift b. Är det att man accepterar i första kontrollen men avvisar i andra kontrollen, eller är det att man avvisar i antingen första ELLER andra kontrollen?
Spontant känns det ändå som att det är första alternativet, dvs, att man accepterar i första men avvisar i andra
Jag tolkar det som andra alternativet. Annars hade väl "avvisa ett parti efter andra kontrollen" varit en bättre formulering.
Men hur kan det gå vidare till kontroll två om det avvisats i kontroll 1? var inte kravet för att det ska komma till kontroll 2 att det först måste accepteras av kontroll 1?
Jo precis, men det skulle kunna vara unionen av sannolikheterna att partierna avvisas i kontroll 1 samt kontroll 2.
Calle_K skrev:Jo precis, men det skulle kunna vara unionen av sannolikheterna att partierna avvisas i kontroll 1 samt kontroll 2.
Ahh okej jo det verkar det vara! Om jag beräknar unionen av händelserna får jag rätt svar:)
Om
A = Händlesen att partiet avvisas i kontroll 1
B = Händelsen att partiet avvisas i kontroll 2
Så det är nog så de menade:) Jag tycker dock det var en lite konstig fråga, för om kontroll 2 ska kunna ske måste ju kontroll 1 ha godkänts:(
B borde ha sannolikheten 0 eftersom man inte kommer till kontroll 2 om man inte klarar kontroll 1. Vi verkar vara helt överens, men kanske inte med uppgiftskonstruktören.
Smaragdalena skrev:B borde ha sannolikheten 0 eftersom man inte kommer till kontroll 2 om man inte klarar kontroll 1. Vi verkar vara helt överens, men kanske inte med uppgiftskonstruktören.
Ja precis egentligen:(
Räkningen blir i slutändan korrekt, men motiveringen är lite fel.
Du har sagt att P(A snitt B) = P(A)P(B) vilket definitivt inte är korrekt, eftersom A och B är högst beroende.
Du kan istället definiera en ny händelse C som händelsen ”klarar kontroll 1 men blir avvisad i kontroll 2”. Då vill vi räkna ut P(A union C) vilket blir P(A) + P(C) eftersom dessa två händelser är disjunkta (de kan inte ske samtidigt).
P(A) är då som tidigare. P(C) är däremot P(klarar kontroll 1)P(avvisad i kontroll 2 | klarar kontroll 1) = (1-P(A))P(avvisad i kontroll 2 | klarar kontroll 1).
Och den andra sannolikheten är vad du kallar för P(B) i din räkning, så som du använt din notation har vi P(C)= (1 - P(A))P(B) (även om du alltså använt P(B) lite fel). Vi får då
P(A union C) = P(A) + (1-P(A))P(B) = P(A) + P(B) -P(A)P(B), alltså exakt det du räknade.
Men som sagt, du använde händelsen B lite fel, samt sa att A och B är oberoende händelser (vilket de inte är). Så jag tror att dessa fel tillsammans ändå laddar i att du får rätt uträkning i slutändan
Hondel skrev:Räkningen blir i slutändan korrekt, men motiveringen är lite fel.
Du har sagt att P(A snitt B) = P(A)P(B) vilket definitivt inte är korrekt, eftersom A och B är högst beroende.
Du kan istället definiera en ny händelse C som händelsen ”klarar kontroll 1 men blir avvisad i kontroll 2”. Då vill vi räkna ut P(A union C) vilket blir P(A) + P(C) eftersom dessa två händelser är disjunkta (de kan inte ske samtidigt).
P(A) är då som tidigare. P(C) är däremot P(klarar kontroll 1)P(avvisad i kontroll 2 | klarar kontroll 1) = (1-P(A))P(avvisad i kontroll 2 | klarar kontroll 1).
Och den andra sannolikheten är vad du kallar för P(B) i din räkning, så som du använt din notation har vi P(C)= (1 - P(A))P(B) (även om du alltså använt P(B) lite fel). Vi får då
P(A union C) = P(A) + (1-P(A))P(B) = P(A) + P(B) -P(A)P(B), alltså exakt det du räknade.
Men som sagt, du använde händelsen B lite fel, samt sa att A och B är oberoende händelser (vilket de inte är). Så jag tror att dessa fel tillsammans ändå laddar i att du får rätt uträkning i slutändan
Ahh det låter mer logiskt tack!:)



