Övningstenta_6_Faktoruppdela polynomet i reella andragradsfaktor

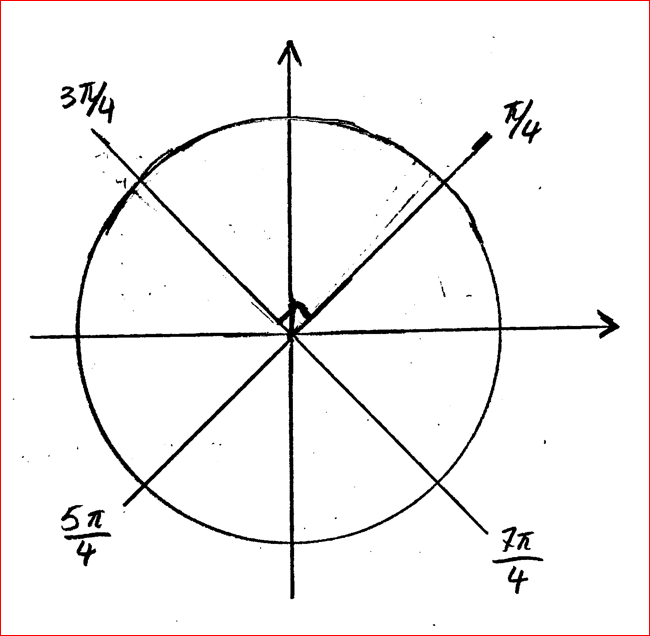
Har du försökt rita upp dem själv i enhetscirkeln? Lägg upp bilden här.

Det du skriver är sant, men (vad jag kan se) så har du bara ritat in vinklaren i en enhetscirkel utan att markera vare sig radien 2 eller koordinaterna på formen z = a+bi.

Smaragdalena skrev:

Det du skriver är sant, men (vad jag kan se) så har du bara ritat in vinklaren i en enhetscirkel utan att markera vare sig radien 2 eller koordinaterna på formen z = a+bi.

Jag har redan skrivit dessa längst upp, när ja ställt frågan. Det ja frågat om är det som du säger hur man kan omvandla dessa vinkelgrader till exakt värde och skriva om de till z=a+bi. 

Det är det jag försöker hjälpa dig med. Börja med det översta uttrycket, det med vinkeln $\frac{3\pi}{4}$. Är du med på att det ligger nånstans på den linjen som ligger i andra  kvadranten?

Det som ja vet är (från min ritning av enhetcirkeln) är i andra kvadranten är cos negativt och sin positivt. 

Ja. Det betyder alltså att i z = a+bi är a negativt och b positivt. Vet du hur man räknar fram att $a=-\sqrt2$ och att $b=\sqrt2$?

Smaragdalena skrev:

Ja. Det betyder alltså att i z = a+bi är a negativt och b positivt. Vet du hur man räknar fram att $a=-\sqrt2$ och att $b=\sqrt2$?

Nej, ja vet inte varför $a=-\sqrt{2} och b =\sqrt{2},$

Dra en linje rakt ner från den punkt där den räta linjen korsar cirkeln i andra kvadranten. Ser du att det blir en rätvinklig likbent triangel, d v s vår gamla bekant "en halv kvadrat"? I uppgiften står det att z₂ = $2e^{i3\pi/4$ och motsvarande tvåa i uttrycket med sinus och cosinus. Den tvåan är absolutbeloppet för vårt komplexa tal, d v s avståndet till origo, eller med antra ord radien på cirkeln = hypotenusan i vår triangel. Hur långa är de båda kateterna i triangeln?

Varför är det så viktigt att låta dessa "komplexkonjugerande rötter" multi. ihop? 

Smaragdalena skrev:

Dra en linje rakt ner från den punkt där den räta linjen korsar cirkeln i andra kvadranten. Ser du att det blir en rätvinklig likbent triangel, d v s vår gamla bekant "en halv kvadrat"? I uppgiften står det att z₂ = $2e^{i3\pi/4$ och motsvarande tvåa i uttrycket med sinus och cosinus. Den tvåan är absolutbeloppet för vårt komplexa tal, d v s avståndet till origo, eller med antra ord radien på cirkeln = hypotenusan i vår triangel. Hur långa är de båda kateterna i triangeln?

Nu är ja helt förvirrad, kan du snälla rita en bild och förklarar med skissen kanske. 

Jag vet inte om du har fått svar på din ursprungsfråga:

Svaret på den frågan kan vi hämta ur din utmärkta bild av enhetscirkeln:

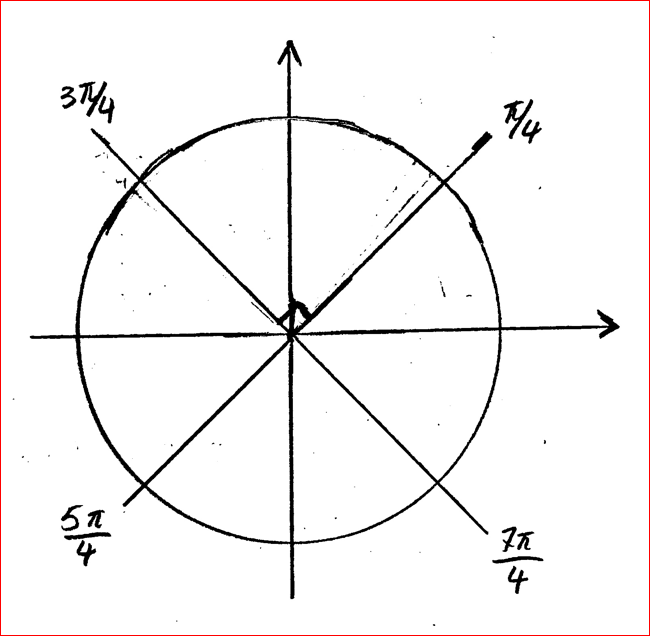
Med hjälp av symmetrin i den och vetskapen att en punkt på enhetscirkeln har koordinaterna (cos(v), sin(v)) kan vi relatera alla de givna trigonometriska värdena till $\sin(\frac{\pi}{4})$ och $\cos(\frac{\pi}{4})$ på följande sätt:

• $\cos(\frac{3\pi}{4})=-\cos(\frac{\pi}{4})$
• $\sin(\frac{3pi}{4})=\sin(\frac{pi}{4})$
• $cos(\frac{5\pi}{4})=-\cos(\frac{\pi}{4})$
• $\sin(\frac{5pi}{4})=-\sin(\frac{pi}{4})$
• $cos(\frac{7\pi}{4})=\cos(\frac{\pi}{4})$
• $\sin(\frac{7pi}{4})=-\sin(\frac{pi}{4})$

Eftersom nu $\sin(\frac{pi}{4})=\frac{\sqrt{2}}{2}$ och $\cos(\frac{pi}{4})=\frac{\sqrt{2}}{2}$ så följer de samband du frågar efter.

Yngve skrev:

Jag vet inte om du har fått svar på din ursprungsfråga:

Svaret på den frågan kan vi hämta ur din utmärkta bild av enhetscirkeln:

Med hjälp av symmetrin i den och vetskapen att en punkt på enhetscirkeln har koordinaterna (cos(v), sin(v)) kan vi relatera alla de givna trigonometriska värdena till $\sin(\frac{\pi}{4})$ och $\cos(\frac{\pi}{4})$ på följande sätt:

• $\cos(\frac{3\pi}{4})=-\cos(\frac{\pi}{4})$
• $\sin(\frac{3pi}{4})=\sin(\frac{pi}{4})$
• $cos(\frac{5\pi}{4})=-\cos(\frac{\pi}{4})$
• $\sin(\frac{5pi}{4})=-\sin(\frac{pi}{4})$
• $cos(\frac{7\pi}{4})=\cos(\frac{\pi}{4})$
• $\sin(\frac{7pi}{4})=-\sin(\frac{pi}{4})$

Eftersom nu $sin(\frac{pi}{4})=\frac[\sqrt{2}{2}$ och $cos(\frac{pi}{4})=\frac[\sqrt{2}{2}$ så följer de samband du frågar efter.

Jag tror ja förstår nu, man kan hitta alla sin och cos värdena m.h.a en cirkelmätare och en bild på enhetcirkeln. 

Marcus N skrev:

Varför är det så viktigt att låta dessa "komplexkonjugerande rötter" multi. ihop? 

Kan någon hjälpa mig med den här frågan också? 

Uppgiften gäller att dela upp polynomet i reella andragradsfaktorer, dvs andragradsfaktorer utan imaginärdel.

Du åstadkommer just det genom att multiplicera ihop de komplexkonjugerade paren av komplexa faktorer.

Detta pga att konjugatregeln (a+b)(a-b) = a²-b² ser till att det ibte blir några blandade termer ab i produkten.

Menar du så här kanske: 

$z*\stackrel{-}{z}=(a+bi)*(a-bi)=a^2+b^2$

Ja, exakt så.