Osäker på hur jag ska räkna

Du kan utnyttja att $\displaystyle -\log(x) = \log(1/x)$.

Löser det sig då?

Jag tror inte Naturens hade gått igenom logaritmlagarna än.

Men det du kan använda är, $a^{-b}=\frac{1}{a^b}$ vilket är samma tips som jag gav dig i förra tråden.

Tack för svaren, nej det stämmer har inte gått igenom de än, det är i nästa kapitel. Förstår inte varför man får uppgifter att göra som liksom kräver att man förstår sådant man inte lärt sig än, men hur som, försöker lösa det ändå. 

10^-Lg12    . Antar att 10^-Lg inte "tar ut varandra" då det är -Lg, annars hade det gått? 
                   Sen tänker jag eftersom att det är -Lg12 så är det, precis som Calle_K skrev förr, 
                   att typ, om det är så att 10^-a blir 1/10a, så... borde då inte 

10^-Ig12                tänker (10^-a=1/10a).     bli det då inte  så att.  10^-Ig12   ska se ut så här:     1/10*12 ?     varför har man annars 10  a i nämnaren? & om 10 i nämnaren är där för att liksom representera hur många 10:or man har så blir de ju 1 hel tia bara.

 Antar att 10^-Lg inte "tar ut varandra" då det är -Lg

Nej, precis. $\log_{10}{x}$ är inversfunktionen till $10^x$. Det betyder bland annat att $\log_{10}{10^x}=x$ och att $10^{\log_{10}{x}}=x$.

Det Calle_K menar är att du kan skriva om $\displaystyle 10^{-\log_{10}{12}}$ till $1/10^{\log_{10}12}$. Då behövs inga logaritmlagar.

okej så, om jag då ska skriva om det hela, tar då 10 och log10 ut varandra i nämnaren så jag bara har 12 kvar där? dvs 

1) 10-Lg12   Samma som 10-Log10  12 
2)10-Log10  12  kan jag skriva om till   1/10 Log10  12 
3) 1/10 Log10  12   Blir 1/12 då 10 i nämnaren och Log10 tar ut varandra?
4)1/12   för att 10 i nämnaren och Log10 tar ut varandra 

Naturens skrev:

okej så, om jag då ska skriva om det hela, tar då 10 och log10 ut varandra i nämnaren så jag bara har 12 kvar där? dvs 

1) 10-Lg12   Samma som 10-Log10  12 

Ja, du kan krångla till det genom att använda icke-standard-skrivsättet log₁₀ i stället för lg.

2)10-Log10  12  kan jag skriva om till   1/10 Log10  12 

Ja, du kan skriva om det till $\frac{1}{{{10}^{{\log }_{10}12}}^{}}$, eller mindre tillkrånglat $\frac{1}{{10}^{lg12}}$.

3) 1/10 Log10  12   Blir 1/12 då 10 i nämnaren och Log10 tar ut varandra?

Menar du $\frac{1}{{10}^{{\log }_{10}12}} =\hspace{0.17em}\frac{1}{{10}^{lg12}}$? I så fall: Ja.

4)1/12   för att 10 i nämnaren och Log10 tar ut varandra 

Ja, det blir 1/12.

Vet inte hur icke-standard eller "tillkrånglat" det är. Jag har väldigt sällan sett "$\mathrm{lg}$" i anglosfären.

Jag tänker så här,

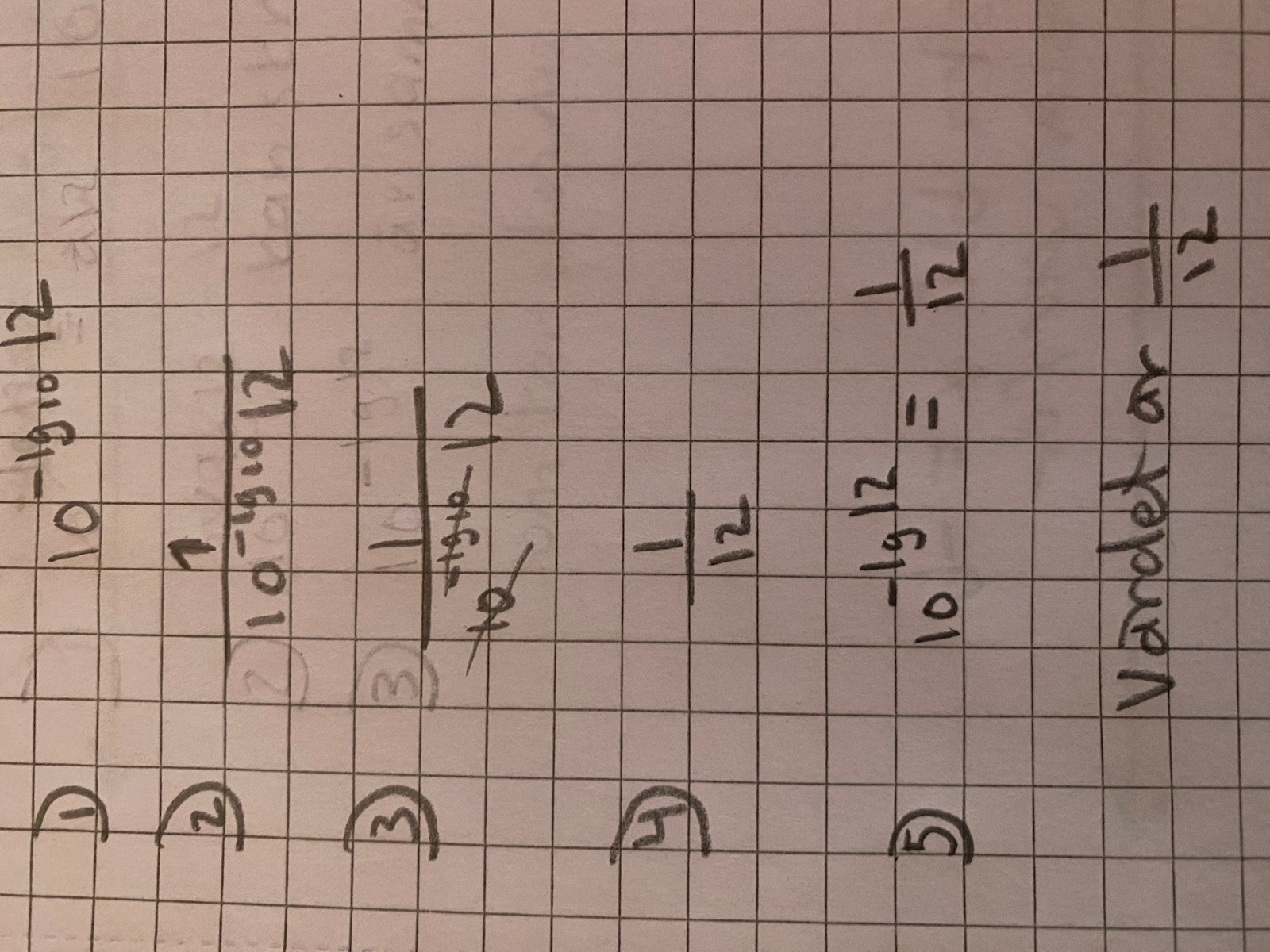
Försöker hitta en förklaring på hur de kan gå från steg 2) till steg 4). Tänker att i steg 4 så har jag bara 12 kvar i nämnaren & det är ju för att 10^  -Log 10 är borta, så tänker hur försvinner det? 

är det för att det är +10 sen ^ till -log 10 dvs är det + & - tecknen som gör att de försvinner. Eller är det, de här som jag har fått lära mig, dvs att:

motsatsen till Log/Lg är 10 upphöjt till något. Här är ju 10 upphöjt till -log10 sen 12, eller upphöjt till -lg 12, så liksom förstår inte riktigt ? 


****
Tillägg undrar hur jag testar detta sen, liksom hur går man från: 
1/12   till   10 ^-Ig  12 

Tillägg undrar hur jag testar detta sen, liksom hur går man från: 1/12 till 10 ^-Ig 12

Det viktigaste är att du inser att 10^lg12 bara är ett (krångligt) sätt att skriva 12.

$\frac{1}{12} = \frac{1}{{10}^{lg12}} = {10}^{-lg12}$. För det sista steget använder du en potenslag, a^-n = 1/aⁿ.

Okej tack