Ortogonal projektion i R3

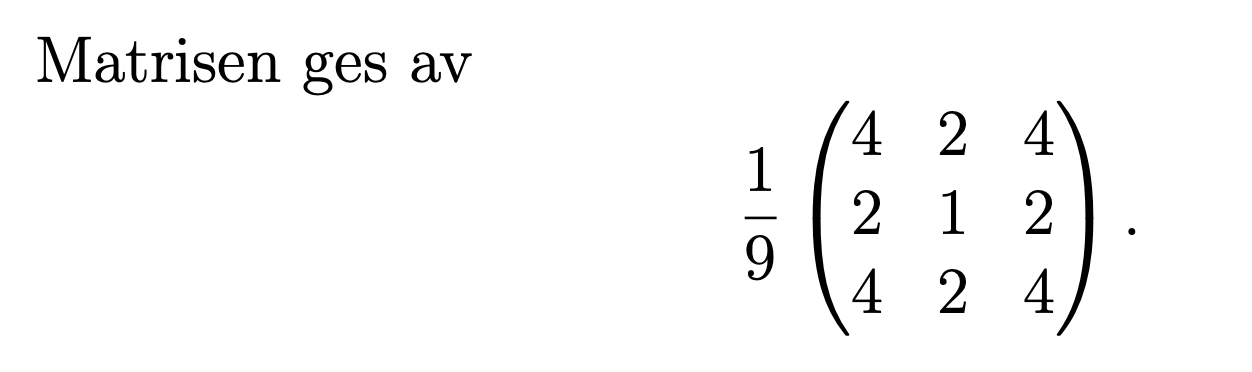
Första frågan är, hur får du fram en avbildningsmatris? Ett sätt är att räkna ut vad avbildningarna av basvektorerna är.

Ortogonal projektion betyder att du projicerar vektorn på linjen. Så, om du projicerar vektorn (1,0,0) på vektorn (2, 1, 2), vad blir det då? Vad händer om du projicerar (0,1,0)? (0,0,1)? Resultaten av dessa projektioner är kolumnerna i avbildningsmatrisen?

Du kan använda dina uträkningar men ersätta x1, x2, x3 med 0 eller 1.

Men i sista steget har du räknat lite fel. Första parentesen (summan) är ett tal, men du har liksom multiplicerat in de olika termerna i summan på de olika elementen i vektorn. 

Här är en alternativ fortsättning, baserat på din uträkning. Du har kommit fram till att:

$\bar{u}=(\bar{p}\cdot \bar{e})\bar{e}$

Det kan vi skriva om som en matris multiplicerat med en vektor (skalärprodukten är symmetrisk):

$\bar{u}=(\bar{p}^t\bar{e})\bar{e}=\bar{e}(\bar{e}^t\bar{p})=\bar{e}\bar{e}^t\,\bar{p}=A\bar{p}$

Nu framgår det tydligt att den i uppgiften sökta matrisen $A=\bar{e}\bar{e}^t$

Hondel skrev:

Första frågan är, hur får du fram en avbildningsmatris? Ett sätt är att räkna ut vad avbildningarna av basvektorerna är.

Ortogonal projektion betyder att du projicerar vektorn på linjen. Så, om du projicerar vektorn (1,0,0) på vektorn (2, 1, 2), vad blir det då? Vad händer om du projicerar (0,1,0)? (0,0,1)? Resultaten av dessa projektioner är kolumnerna i avbildningsmatrisen?

Stort tack! Nu har jag löst uppgiften med denna metod. En liten fråga bara: när man tar fram en avbildningsmatris på detta vis, finns det någon föredragen variabel att använda för att hänvisa till e1, e2 och e3 (standardbasvektorerna) efter de avbildats? Eller kallar man dem F(e1), F(e2) och F(e3) ?

D4NIEL skrev:

Här är en alternativ fortsättning, baserat på din uträkning. Du har kommit fram till att:

$\bar{u}=(\bar{p}\cdot \bar{e})\bar{e}$

Det kan vi skriva om som en matris multiplicerat med en vektor (skalärprodukten är symmetrisk):

$\bar{u}=(\bar{p}^t\bar{e})\bar{e}=\bar{e}(\bar{e}^t\bar{p})=\bar{e}\bar{e}^t\,\bar{p}=A\bar{p}$

Nu framgår det tydligt att den i uppgiften sökta matrisen $A=\bar{e}\bar{e}^t$

Tack! Men jag är inte riktigt med på tankegången. Hur kommer det sig att vi tar p-transponat gånger e? Och hur kan vi sedan komma fram till att e*e transponat är samma sak som matrisen A?

starboy skrev:

Hondel skrev:

Första frågan är, hur får du fram en avbildningsmatris? Ett sätt är att räkna ut vad avbildningarna av basvektorerna är.

Ortogonal projektion betyder att du projicerar vektorn på linjen. Så, om du projicerar vektorn (1,0,0) på vektorn (2, 1, 2), vad blir det då? Vad händer om du projicerar (0,1,0)? (0,0,1)? Resultaten av dessa projektioner är kolumnerna i avbildningsmatrisen?

Stort tack! Nu har jag löst uppgiften med denna metod. En liten fråga bara: när man tar fram en avbildningsmatris på detta vis, finns det någon föredragen variabel att använda för att hänvisa till e1, e2 och e3 (standardbasvektorerna) efter de avbildats? Eller kallar man dem F(e1), F(e2) och F(e3) ?

F(e1) osv låter väl bra :)

starboy skrev:

D4NIEL skrev:

Här är en alternativ fortsättning, baserat på din uträkning. Du har kommit fram till att:

$\bar{u}=(\bar{p}\cdot \bar{e})\bar{e}$

Det kan vi skriva om som en matris multiplicerat med en vektor (skalärprodukten är symmetrisk):

$\bar{u}=(\bar{p}^t\bar{e})\bar{e}=\bar{e}(\bar{e}^t\bar{p})=\bar{e}\bar{e}^t\,\bar{p}=A\bar{p}$

Nu framgår det tydligt att den i uppgiften sökta matrisen $A=\bar{e}\bar{e}^t$

Tack! Men jag är inte riktigt med på tankegången. Hur kommer det sig att vi tar p-transponat gånger e? Och hur kan vi sedan komma fram till att e*e transponat är samma sak som matrisen A?

Man kan se vektorer som $3\mathrm{x}1$-matriser. Om man då transponerar en vektor får man en $1\mathrm{x}3$-matris. Skalärprodukten mellan två vektorer är just en operation där man transponerar den första vektorn och matrismultiplicerar den med den andra vektorn. Låt oss beräkna längden $\bar{u}\cdot \bar{u}$ exempel:

$\bar{u}\cdot \bar{u}=(2,1,2)^t(2,1,2)=\left( \begin{array}{ccc} 2 & 1 & 2\end{array} \right) \left( \begin{array}{c} 2 \\ 1 \\ 2\end{array} \right)=4+1+4=9$

Eftersom $\bar{p}\cdot \bar{e}=\bar{e}\cdot \bar{p}$ och det bara är en skalär kan vi ordna om så att

$(\bar{p}^t\bar{e})\bar{e}=\bar{e}(\bar{e}^t\bar{p})=\bar{e}\bar{e}^t\,\bar{p}$

Men $\bar{e}\bar{e}^t$ är ju enligt matrisalgebrans regler en matris av storlek $3\mathrm{x}3$

$\bar{e}\bar{e}^t=\frac{1}{9}\left( \begin{array}{c} 2 \\ 1 \\ 2\end{array} \right) \left( \begin{array}{ccc} 2 & 1 & 2\end{array} \right)=\frac{1}{9}\left(\begin{array}{ccc} 4 & 2 & 4 \\ 2 & 1 & 2 \\ 4 & 2 & 4 \end{array}\right)$

D4NIEL skrev:

starboy skrev:

Visa föregående citat

D4NIEL skrev:

Här är en alternativ fortsättning, baserat på din uträkning. Du har kommit fram till att:

$\bar{u}=(\bar{p}\cdot \bar{e})\bar{e}$

Det kan vi skriva om som en matris multiplicerat med en vektor (skalärprodukten är symmetrisk):

$\bar{u}=(\bar{p}^t\bar{e})\bar{e}=\bar{e}(\bar{e}^t\bar{p})=\bar{e}\bar{e}^t\,\bar{p}=A\bar{p}$

Nu framgår det tydligt att den i uppgiften sökta matrisen $A=\bar{e}\bar{e}^t$

Tack! Men jag är inte riktigt med på tankegången. Hur kommer det sig att vi tar p-transponat gånger e? Och hur kan vi sedan komma fram till att e*e transponat är samma sak som matrisen A?

Man kan se vektorer som $3\mathrm{x}1$-matriser. Om man då transponerar en vektor får man en $1\mathrm{x}3$-matris. Skalärprodukten mellan två vektorer är just en operation där man transponerar den första vektorn och matrismultiplicerar den med den andra vektorn. Låt oss beräkna längden $\bar{u}\cdot \bar{u}$ exempel:

$\bar{u}\cdot \bar{u}=(2,1,2)^t(2,1,2)=\left( \begin{array}{ccc} 2 & 1 & 2\end{array} \right) \left( \begin{array}{c} 2 \\ 1 \\ 2\end{array} \right)=4+1+4=9$

Eftersom $\bar{p}\cdot \bar{e}=\bar{e}\cdot \bar{p}$ och det bara är en skalär kan vi ordna om så att

$(\bar{p}^t\bar{e})\bar{e}=\bar{e}(\bar{e}^t\bar{p})=\bar{e}\bar{e}^t\,\bar{p}$

Men $\bar{e}\bar{e}^t$ är ju enligt matrisalgebrans regler en matris av storlek $3\mathrm{x}3$

$\bar{e}\bar{e}^t=\frac{1}{9}\left( \begin{array}{c} 2 \\ 1 \\ 2\end{array} \right) \left( \begin{array}{ccc} 2 & 1 & 2\end{array} \right)=\frac{1}{9}\left(\begin{array}{ccc} 4 & 2 & 4 \\ 2 & 1 & 2 \\ 4 & 2 & 4 \end{array}\right)$

Stort tack! Fin förklaring