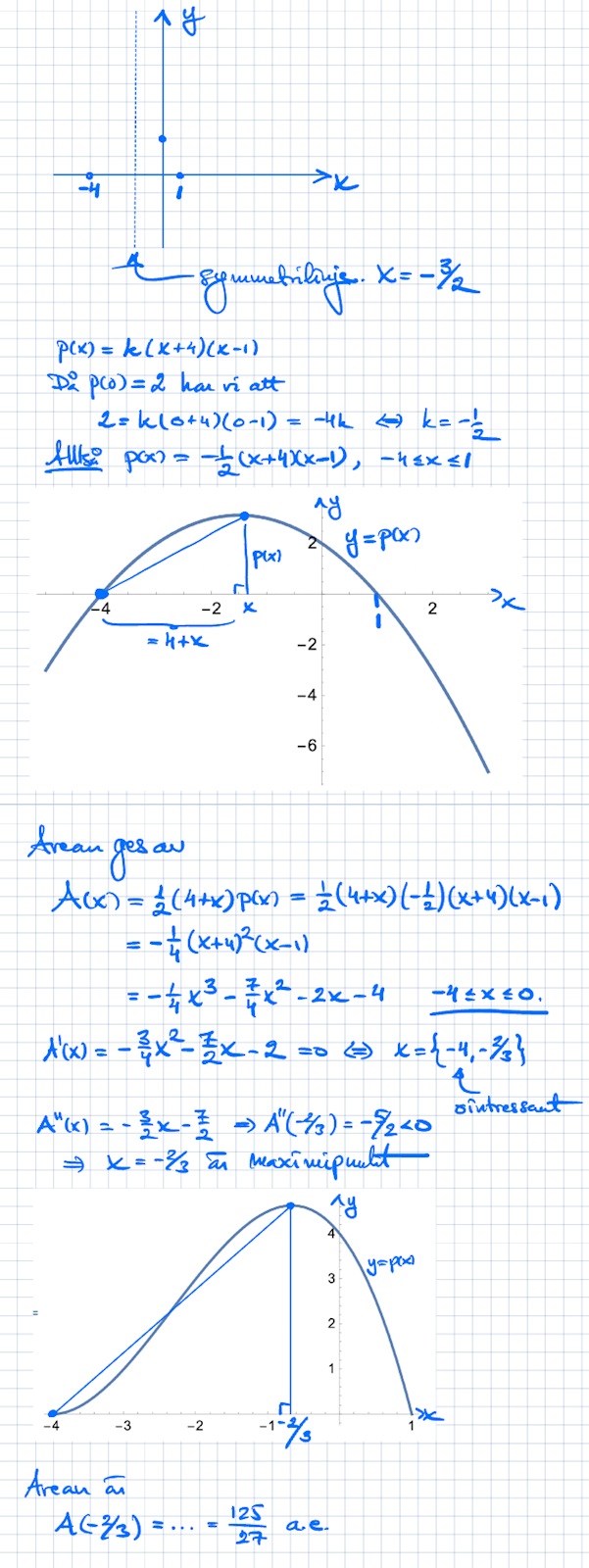
Optimeringsproblem - Bestäm area av största triangel
Hej, jag har försökt lösa denna uppgift men får fel svar, vart har jag gjort fel?
Arean ska vara (5/3)^3 a.e.
Här är uppgiften och min lösning:


Jag höll på med en lösning, men blev avbruten. Ser att Trinity2 fixat det.
När du skriver arean skriver du basen som (4+x), jag skrev endast x, varför blir mitt fel? Vi har lärt oss att lösa sådana uppgifter med x i basen av triangeln, att hela basen är x.
Och varför är x=-4 ointressant?
Längden från origo till -4 är 4 l.e.
x är negativt, t.ex. -1.5 och avståndet från -4 till x är då 4+x = 4 + (-1.5) = 2.5
x=-4 ger ej upphov till en triangel. Höjden = 0 för detta fall. Samma sak gäller för x=1, men uppgiften sa att vi var i 2:a kvadranten så x≤0.
Okej, tack så mycket, jag förstår. Men varför kan man inte sätta den sträcka som x kan vara som bara x? Det borde ge samma svar tycker jag.
Alexandra06 skrev:Okej, tack så mycket, jag förstår. Men varför kan man inte sätta den sträcka som x kan vara som bara x? Det borde ge samma svar tycker jag.
Om vi låter basen vara x lång (räknat från -4), då blir den räta vinkelns position på x-axeln -4+x och det är det vi måste ange i p(x-4) för att få höjden. Slutresultatet skall bli detsamma.
Avståndet från b till a (om a är störst) är a–b
Här har vi avståndet från –4 till x, alltså x–(–4) = x+4
En sista fråga om den här uppgiften. När du har förenllat klart A(x) får du termen -4, hur kommer det sig? Jag får den positiv, får exakt som du fast termen blir positiv. 4 (-4) = -16 -> -16/-4 = 4
Alexandra06 skrev:En sista fråga om den här uppgiften. När du har förenllat klart A(x) får du termen -4, hur kommer det sig? Jag får den positiv, får exakt som du fast termen blir positiv. 4 (-4) = -16 -> -16/-4 = 4
Ett skrivfel av mig. Det skall vara +. Bra observerat!
Och, i den sista grafen har jag dragit en hypotenusa. Det är bara dumheter. Bortse från den. Grafen visar arean, och dess maximum. Det är parabeln i grafen tidigare som har en triangel, INTE den andra grafen.
Okej tack. Skulle man kunna ha basen på triangeln som x och höjden f(x-4), alltså i A(x)?
Och är det alltid så att om nollsttället och triangelns ena hörn är negativ att hela basen blir x-nollstället? Borde det inte vara + istället? Alltså x+(-4) eller är det -?
Alexandra06 skrev:Okej tack. Skulle man kunna ha basen på triangeln som x och höjden f(x-4), alltså i A(x)?
Och är det alltid så att om nollsttället och triangelns ena hörn är negativ att hela basen blir x-nollstället? Borde det inte vara + istället? Alltså x+(-4) eller är det -?
Ja, se #7.
Se #8 som förklarar avstånd bra.
Tack så mycket, missade det.