öppen och sluten mängd (flervariabelanalys)

Båda är slutna mängder. En sluten mängd innebär helt enkelt att randen är inkluderad i området. Exempel: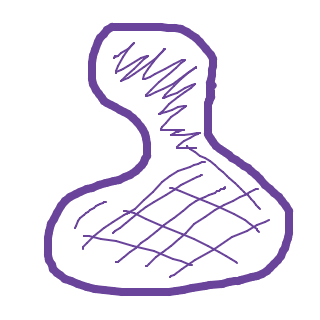

I detta område är randen inkluderad (en inkluderad rand brukar ritas med en linje, medan en exkluderad rand brukar ritas streckad). I området nedan är randen utesluten: 

Ett trick för att undersöka om randen ingår eller inte på ett mer matematiskt sätt, är att försöka närma sig den. Vi ritar ett område i ett koordinatsystem:

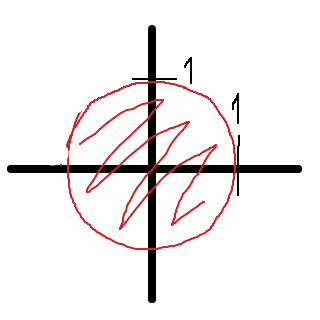
Vi tänker nu att vi ska försöka hitta de värden som ligger längst ut, men fortfarande inuti området. Om vår yta eller mängd är sluten är detta mycket enkelt, då är punkterna längst ut men fortfarande inuti området lika med den cirkel som innesluter området, $x^2+y^2=1$. Hur blir det då om vi har ett öppet område? Vilka punkter ligger ytterst? Vi kan konstatera att punkterna på cirkeln $x^2+y^2=0,9$ ligger inuti området och en bra bit från mitten, men de kan ju inte vara ytterst, eftersom punkterna på cirkeln $x^2+y^2=0,99$ ligger längre ut. Vi kan konstatera att punkterna i denna cirkel ligger inuti området och en bra bit från mitten, men de kan ju inte vara ytterst, eftersom punkterna på cirkeln $x^2+y^2=0,999$ ligger längre ut. Och så fortsätter det. Har vi en sluten mängd kan vi lätt se vilka punkter som ligger ytterst, men om vi har en öppen mängd kan vi inte hitta de yttersta punkterna. 

Motsatsen kan också undersökas, vilka punkter ligger närmast området, men ändå utanför? Vad händer om du använder samma metod som ovan, men för att hitta dessa punkter? :)

Den första mängden är sluten eftersom den är begränsad och randen ingår. Hur är det med den andra mängden?

Smutstvätt skrev:

Båda är slutna mängder. En sluten mängd innebär helt enkelt att randen är inkluderad i området. Exempel:

I detta område är randen inkluderad (en inkluderad rand brukar ritas med en linje, medan en exkluderad rand brukar ritas streckad). I området nedan är randen utesluten: 

Ett trick för att undersöka om randen ingår eller inte på ett mer matematiskt sätt, är att försöka närma sig den. Vi ritar ett område i ett koordinatsystem:

Vi tänker nu att vi ska försöka hitta de värden som ligger längst ut, men fortfarande inuti området. Om vår yta eller mängd är sluten är detta mycket enkelt, då är punkterna längst ut men fortfarande inuti området lika med den cirkel som innesluter området, $x^2+y^2=1$. Hur blir det då om vi har ett öppet område? Vilka punkter ligger ytterst? Vi kan konstatera att punkterna på cirkeln $x^2+y^2=0,9$ ligger inuti området och en bra bit från mitten, men de kan ju inte vara ytterst, eftersom punkterna på cirkeln $x^2+y^2=0,99$ ligger längre ut. Vi kan konstatera att punkterna i denna cirkel ligger inuti området och en bra bit från mitten, men de kan ju inte vara ytterst, eftersom punkterna på cirkeln $x^2+y^2=0,999$ ligger längre ut. Och så fortsätter det. Har vi en sluten mängd kan vi lätt se vilka punkter som ligger ytterst, men om vi har en öppen mängd kan vi inte hitta de yttersta punkterna. 

Motsatsen kan också undersökas, vilka punkter ligger närmast området, men ändå utanför? Vad händer om du använder samma metod som ovan, men för att hitta dessa punkter? :)

okej men då är det väl inget man räknar på för om man får en olikhet eller likhet så ser man på det intervallet om den är sluten eller öppen i så fall? dvs om ändpunkterna ingår eller icke

då är jag också med på att en mängd är sluten om dess komplement är öppen, för man kan i så falla från komplement sida komma oändligt nära randen?

men om ett område är öppet då borde väl dess komplement också kunna vara öppet? eller är det i så fall samma mängd?

Smutstvätt skrev:

Båda är slutna mängder.

Nej. Vilket är det största värdet som x kan anta i den andra mängden?

okej men då är det väl inget man räknar på för om man får en olikhet eller likhet så ser man på det intervallet om den är sluten eller öppen i så fall? dvs om ändpunkterna ingår eller icke

Det stämmer, randen brukar i princip alltid framgå av definitionen av mängden. :) 

då är jag också med på att en mängd är sluten om dess komplement är öppen, för man kan i så falla från komplement sida komma oändligt nära randen?

Jajamen!

men om ett område är öppet då borde väl dess komplement också kunna vara öppet? eller är det i så fall samma mängd?

Nja, inte riktigt. Komplementet till mängden innehåller ju allting som mängden inte innehåller. Om mängden är öppen innehåller den inte sin rand, och därmed måste komplementet innehålla randen. 

Smutstvätt skrev:

okej men då är det väl inget man räknar på för om man får en olikhet eller likhet så ser man på det intervallet om den är sluten eller öppen i så fall? dvs om ändpunkterna ingår eller icke

Det stämmer, randen brukar i princip alltid framgå av definitionen av mängden. :) 

då är jag också med på att en mängd är sluten om dess komplement är öppen, för man kan i så falla från komplement sida komma oändligt nära randen?

Jajamen!

men om ett område är öppet då borde väl dess komplement också kunna vara öppet? eller är det i så fall samma mängd?

Nja, inte riktigt. Komplementet till mängden innehåller ju allting som mängden inte innehåller. Om mängden är öppen innehåller den inte sin rand, och därmed måste komplementet innehålla randen. 

okej tusen tack för hjälpen då är jag med!!

Smaragdalena skrev:

Smutstvätt skrev:

Båda är slutna mängder.

Nej. Vilket är det största värdet som x kan anta i den andra mängden?

Det finns inget sådant, men det finns ett minsta värde x kan anta. I sådant fall är väl inte den första mängden sluten heller, eftersom det inte finns något "lock" som övre gräns? Eller har jag förvirrat mig själv helt nu? När jag läste om öppna och slutna mängder fick jag lära mig att exempelvis mängden $x\in\mathbb{R},\;x\geq5$ var en sluten mängd, men det kanske är jag som minns fel? 

Maremare skrev:

okej tusen tack för hjälpen då är jag med!!

Varsågod! Jag och Smaragdalena diskuterar lite kring de exempel du nämnt, och jag misstänker att Smaggan har rätt, som vanligt. $🥺$ Men teorin i denna tråd är korrekt i alla fall. :)

En delmängd är sluten om och endast om dess komplement är öppet. Tex är hela ${\mathrm{ℝ}}^3$ både en öppen och en sluten mängd.

Tex är komplementet (i R) till x $\ge$5 mängden x < 5, som är öppen eftersom kring varje punkt vi kan finna en liten omgiving som ligger helt i mängden.

Jag tror Smaragdalena tänker på kompakt mängd, vilket i R³ är ekvivalent med att vara både sluten och begränsad.

Jag tror Smaragdalena tänker på kompakt mängd, vilket i R³ är ekvivalent med att vara både sluten och begränsad.

Du har nog rätt. 

Så, bara för att ge lite klarhet i Maremares exempel, de är båda slutna? :)