Omvänt variabelbyte
Jag ska beräkna båglängden för y=x^2 fån x=0 till x=2
Så här långt har jag kommit men är helt fast nu, någon med förslag?
Boken hoppar direkt till integralen nu men jag hänger inte med:/

Det är inte 'konstigt' du inte hänger med för den integralen är inte helt lätt att beräkna snabbt. Det ser ut som en 'amerikansk lösning' och de älskar 'sec' och andra trigonometriska avtarer och många av dessa, typ sec^3, är standardintegraler som de lär sig utantill. I svensk skola är dessa sällsynta och deras analytiska lösning är mera komplicerad. T.ex. anv. man reduktionsformeln
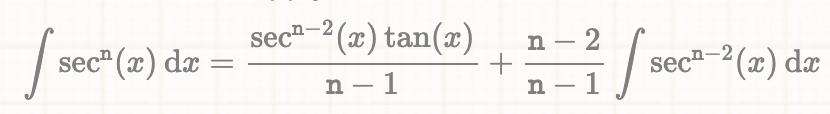
för att sänka gradtalet och sedan är sec en standard integral;
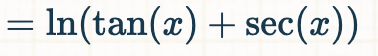
och sedan kombinerar man ihop detta. Men långt ifrån "rakt fram" som det är i lösningen.
Jag tycker det verkar vara en onödigt krånglig substitution, särskilt om man måste beräkna manuellt. Man kan istället utnyttja att integralen återkommer vid partiell integration. Ungefär så här (Partiell integration och lägg till +1-1)
Notera hur integralen återkom! Vi utnyttjade också standardintegralen . Nu kan vi flytta över till VL och får då
Första gången jag såg det här tricket under grundkursen för en liknande integral blev jag så imponerad att det numera sitter i ryggraden :)
Tack så mycket för hjälpen!!
Ja min bok är så förtjust i sec vilket (som tur är) min examinator inte är. Det med I hade jag inte ens tänkt på då vi hastigt gick igenom den ett tag sen. Måste repeteras innan tentan...
Återigen, tack för hjälpen!

