Om jag fattat diffrentialekvationer rätt så bör detta vara rätt tänk.

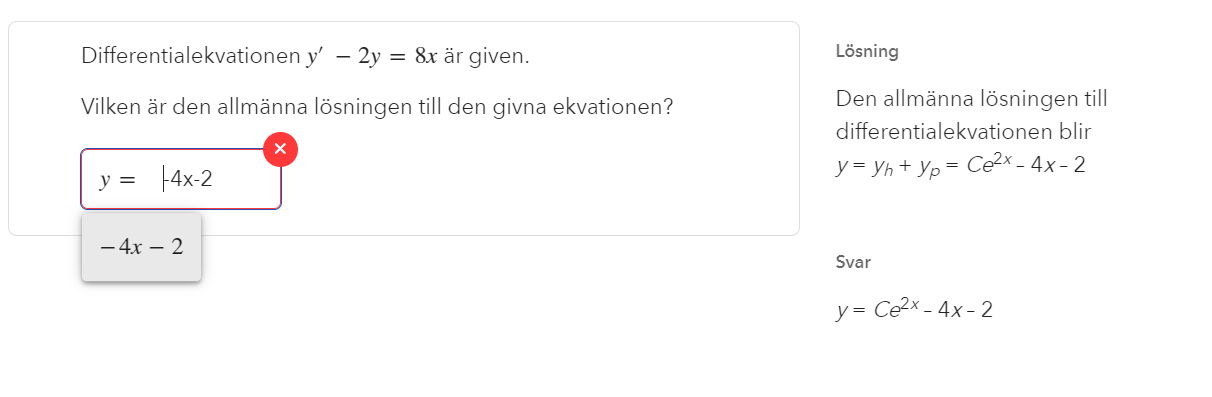Ce^(2x) är den allmänna homogena lösningen, och den agerar som ett start värde till den inhomogena lösningen, dvs där y = 0

f(x)=y'-2y
f(x)=0=Ce^(2x), man kan säga att den homogen lösningen i detta fall är ett ökat värde på y=ax +b +C

Vi vet sedan genom prövning att en inhomogen partikulär lösning kan skrivas y=-4x-2, men den allmänna skulle även få ett extra värde som beror av vi vet att den inhomogena lösningen skär x axeln vid den homogena lösningen, värde som kan variera, som även beror på x.

Funktionen får då det förökade potentiella värde Ce^(2x)

Så: y=-4x-2+Ce^(2x), blir den allmänna lösningen?