Olja i sfär

Du måste hitta ett uttryck för hur snabbt vätskehöjden i tanken ökar som funktion av tiden, dvs $\frac{dh}{dt}$. Uppgiften ger dig hur snabbt man pumpar in olja i tanken, dvs $\frac{dV}{dt}$. Vilket samband finns mellan $\frac{dV}{dt}$ och $\frac{dh}{dt}$?

$\frac{dV}{dT }= \frac{dV}{dH}x \frac{dH}{dT}$

dV/dT = 25 l/min

Menar du detta?

Tillägg: 27 jan 2024 17:54

Man efterfrågar dH/dT väl?

Jo, maN efterfrågar dh/dt. Därför måste du på två olika sätt, ett i a och ett annat i b, räkna fram dV/dh.

Kommer du vidare?

FOrmeln för en sfär är $\frac{4{\mathrm{\pi r}}^3}{3}$, och om man deriverar denna:

4(pi)rˆ2

Men eftersom v beror på h, så antar jag att man utifrån radien kan få fram ett uttryck på h? Hurdå? är frågan nu

Ja, en svårighet är att hitta ett uttryck för $\frac{dV}{dh}$. Det du gjorde härovan var att försöka beräkna $\frac{dV}{dR}$, men det leder dig ingen vart eftersom R är en konstant (tanken ändrar inte volym).

Men nu har du förstått vad uppgiften går ut på, vilket är ett bra steg i rätt riktning. 

I a-uppgiften ger man tipset att beräkna volymen $∆V$ hos en tunn skiva av tanken, en skiva med tjockleken $∆h$. Om vi lyckas med det (vilket vi såklart kommer att göra...) så kan vi skapa ett uttryck för $\frac{∆V}{∆h}$, vilket blir samma sak som $\frac{dV}{dh}$ om $∆h$ är mycket litet.

Hur ska du då göra för att härleda detta uttryck? Börja med att rita en bild av tanken, och fundera på om du kan uttrycka "snittarean" av den tunna skivan vid höjden h, som en funktion av h.

Ja, en svårighet är att hitta ett uttryck för dVdh���ℎ. Det du gjorde härovan var att försöka beräkna dVdR����, men det leder dig ingen vart eftersom R är en konstant (tanken ändrar inte volym).

Ah okej, fattar vad du menar. Men varför skulle det inte gå att uttrycka R mha höjden? FÖr H är väl inte konstant? (oljenivån ändras)

Hur ska du då göra för att härleda detta uttryck? Börja med att rita en bild av tanken, och fundera på om du kan uttrycka "snittarean" av den tunna skivan vid höjden h, som en funktion av h.

Kan jag utgå från frågans figur? Jag kommer tyvärr inte på hur jag kan uttrycka denna "snittarea" och hur jag med det ska uttrycka dv/dh.

Men varför skulle det inte gå att uttrycka R mha höjden? FÖr H är väl inte konstant? (oljenivån ändras)

Jo, men R är konstant, och ditt V är tankens volym. Det V som du måste hitta är oljans volym.

Kan jag utgå från frågans figur?

Jättebra ide! Då slipper man ägna tid åt att försöka rita en bra figur. Jag kan rita in några viktiga linjer med mått, så kanske det hjälper dig lite. Ser du hur jag har kommit fram till nedanstående figur, och ser du hur du nu kan teckna arean av vätskeytan som funktion av $h$?

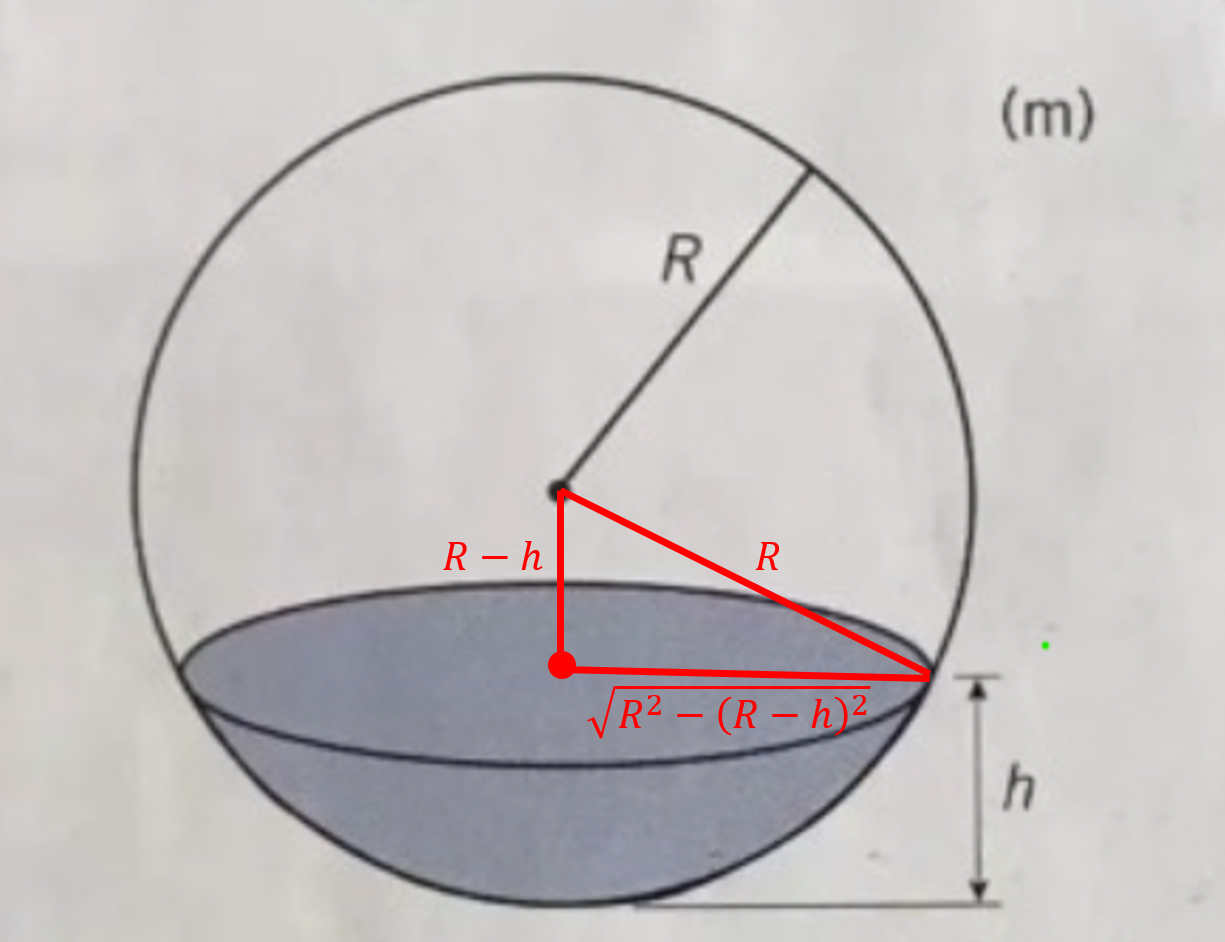
R Är 5m (hypotenusa)

R-H = 5-0,5 = 4,5m (vertikala katet)

horisontella katet är $\sqrt{4,75}$m

Vad är det vi har räknat ut? Är det radien för oljans volym? Kanske lite dum fråga men varför vill vi ha denna? Edit: Ah, för att vi vill ha hastigheten just vid ett tillfälle hur snabbt det stiger?

Arean: 4(pi)r²

vilket dock är en funktion av r

Arean av vätskeytan vid höjden $h$ är alltså

$A_{surface}=\pi r^2=\pi ·\left(R^2-{\left(R-h\right)}^2\right)=\pi ·\left(R^2-\left(R^2-2Rh+h^2\right)\right)=\pi ·\left(2Rh-h^2\right)$

och volymen $∆V$ av en vätskeskiva med tjockleken $∆h$ blir

$∆V=∆h·A_{surface}=∆h\mathrm{\pi }\left(2\mathrm{Rh}-{\mathrm{h}}^2\right)$

$\frac{∆V}{∆h}=\mathrm{\pi }\left(2\mathrm{Rh}-{\mathrm{h}}^2\right)$

Alltså 

$\frac{dV}{dh}=\mathrm{\pi }\left(2\mathrm{Rh}-{\mathrm{h}}^2\right)$

Lyckades lösa uppgiften, men förstår inte en del steg.

1. Varför räknar vi ut radien för oljenivån? Jag är med på hur den fås fram men inte varför man vill ha den.

2. Varför tar man arean av en cirkel (varför räknar man arean)? Javisst det kanske är för man ska tänka att det är en cylindrisk skiva men jag tycker frågeställningen var litegrann skev?

3. Hur kommer delta(h) in? Arean för en cirkel är bara (pi)rˆ2. Förstår att delta(h) är tjockleken på denna skiva men inte hur den "tas" in? Är det från "cylinders volym" formeln? 

Därför att för att kunna utnyttja det matematiska sambandet mellan oljevolymens $\frac{dV}{dt}$ och oljenivåns $\frac{dh}{dt}$ så måste man veta hur $h$ förändras när $V$ förändras, dvs $\frac{dV}{dh}$. Och $\frac{dV}{dh}$ kan man undersöka genom att observera vad som händer med $V$ om man gör en liten förändring av $h$, med sambandet ${∆V}_{olja}\approx A_{oljeyta}·∆h$.

Jag skriver "ungefär lika med" eftersom, precis som du säger, det blir lite "skevt". Likheten uppstår först när man låter$∆h\to dh$. Du gör precis samma sak när du beräknar rotationsvolymer kring y-axeln, då du på samma sätt beräknar volymen av en tunn skiva med tjockleken $dy$ (som du sedan summerar över y-intervallet med hjälp av integralen)  

Tack snälla!

Hur blir det med (b)? SKulle jag kunna få vägledning

På b-uppgiften får du funktionen $V\left(h\right)$ gratis i uppgifttexten. Prova att beräkna $V\text{'}\left(h\right)$och jämför med uttrycket vi tillsammans härledde i a-uppgiften.

Ja just det. Efter derivering och insättning av 5dm och 50dm så får jag samma svar på båda.

Tack för din hjälp!