Olikhet

Jag fattar inte riktigt hur jag ska beskriva arean med en olikhet.
Tänkte först A=b•h/2
(Basen) -5<x<15
(Höjden) -5<y<15
Fast det verkar jättefel. Kan nån förklara?
Tack på förhand
Man ska hålla sig under den sneda linjen
och til höger om den lodräta
och ovanför den vågräta.
Möjligen ingår även linjerna i det sökta området.
Det är inte lätt att se vilket som gäller.
Punkterna på den vågräta linjer uppfyller villkoret y = -5
Punkterna ovanför den vågräta linjer uppfyller villkoret y > -5
Punkterna under den vågräta linjer uppfyller villkoret y < -5
Vilken/vilka av dem gäller för punkterna i den bruna området?
etc
Man behöver därför tre olikheter för att beskriva området.
Vänta, så jag behöver inte skriva en olikhet för varje linje?
Du har förstått att x ligger mellan två x-värden: -5 och 15, alltså -5 < x < 15. På samma sätt ligger y mellan två y-värden, men som vi ser i figuren så förändras översta gränsen för y-värdet. Hur beror förändringen på x? Till exempel när x = 0 är -5 < y < 10 medan vid x = 5 är -5 < y < 5.
Asså y:s ekvation är ju bara linjens funktion eller?? Kan man tänka så
Det behövs som sagt tre olikheter, och det blir enklast om varje olikhet tar hand om bara en linje. Arean behöver du inte bry dig om.
Ta t.ex. den vågräta linjen. Vad har den för ekvation? Vilken olikhet gäller för allt som ligger ovanför den?
Det fungerar att tänka så. Övre gränsen blir alltså linjens y-värde vid ett specifikt x-värde.
Jag fattar inte riktigt.
Basen och höjden har samma olikhet?!
Vad har då Hypotenusan för olikhet?
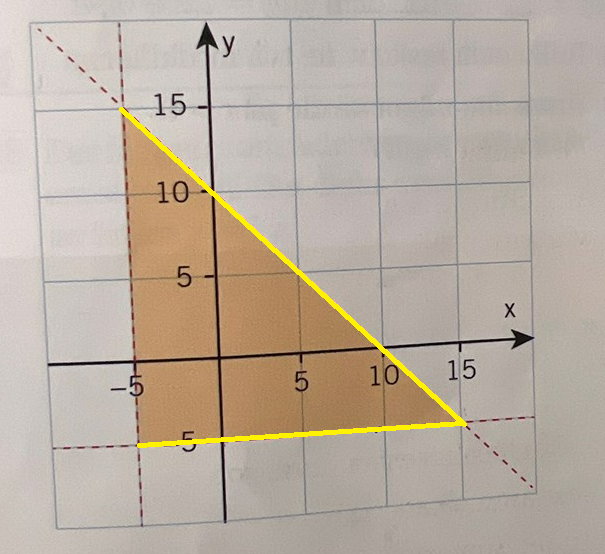 Om vi kollar på olikheten för y så är den nedre linjen den nedre gränsen och den sneda linjen den övre gränsen. Värdet på den nedre kommer inte att ändras, den förblir ju y = -5 för alla x-värden. Men den övre gränsen varierar, den minskar ju större x är. Hur varierar den med x? (vad har den övre gränsen för funktion?)
Om vi kollar på olikheten för y så är den nedre linjen den nedre gränsen och den sneda linjen den övre gränsen. Värdet på den nedre kommer inte att ändras, den förblir ju y = -5 för alla x-värden. Men den övre gränsen varierar, den minskar ju större x är. Hur varierar den med x? (vad har den övre gränsen för funktion?)


