Olikhet
Gammal tentauppgift i envarre:
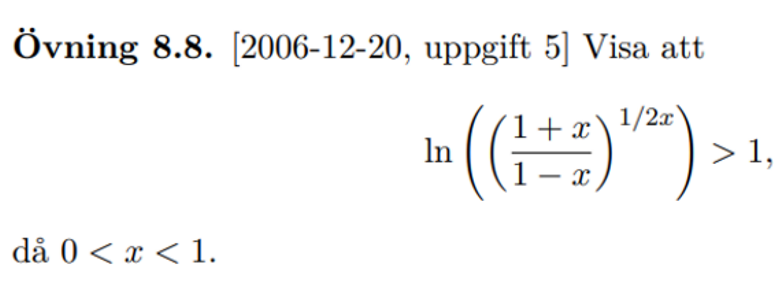
Jag har konstaterat att limx-->0 = 1 enligt:
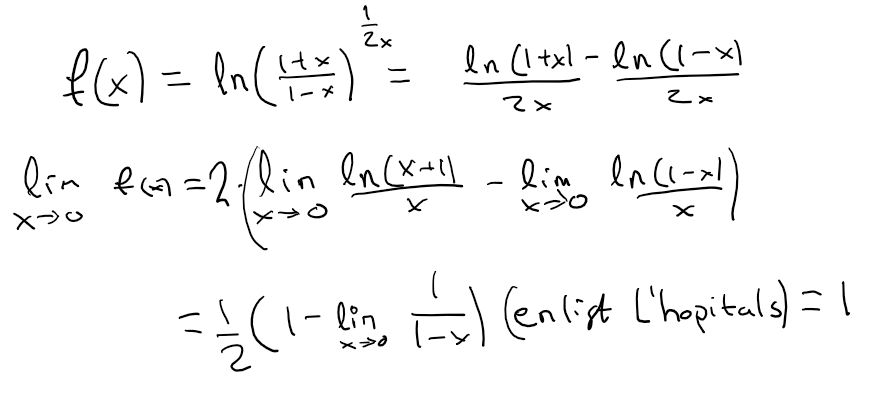
Men det återstår att bevisa att funktionen är växande i (0,1). f' har jag även fått fram som har formen:
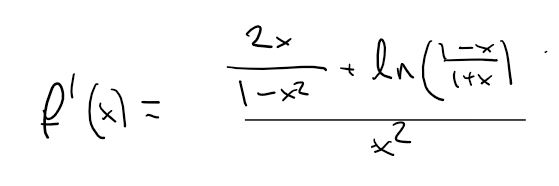
Vilket är rätt efter dubbelkoll med desmos. Ekvationen f'(x)=0 är däremot väldigt svår att lösa. Den enda roten är x=0 som är minpunkt, men det vet jag bara eftersom jag kikade på dess graf. Kanske att man kan gissa sig till den roten på tentan, men hur visar man isåfall att det inte finns fler rötter i (0,1)? Eller finns det något annat smart sätt att lösa uppgiften?
Du skriver ”Jag har konstaterat att limx-->0 = 1 ” och det förstår jag inte. Går x mot 1 när det går mot 0??
Jag ska se om jag kommer någon vart med olikheten.
Jag menar att lim x-->0 f(x)=1
Påståendet är ekvivalent med att uttr innanför ln-parentesen är större än e.
[(1+x)1/(2x) / (1–x)1/(2x) ] ska visas vara > e när 0 < x < 1
sätt 1/(2x) = t; t > 1/2, ger x = 1/(2t)
[(1 + 1/(2t))t / (1 – 1/(2t))t ] = (dela täljare och nämnare med t) =
[ (1 + 0,5 / t)t / t ] / [ ( 1 + (–0,5)/t )t / t]
När t går mot infinity gåt nämnare och täljare mot e0,5 respektive e–0,5
så kvoten går mot e.
Men det räcker ju inte, vi ska visa att kvoten hela tiden är större än e.
Nu har min telefon plingat en stund. Jag kommer inte längre just nu, hoppas det gav något.

