Numerisk bestämning av luftmotståndkoefficient

Hej!
Vi har som uppgift att bestämma luftmotståndkoefficienten experimentellt och vad som påverkar den. Till vår hjälp har vi kameror som analyserar pendelns postition samt hastighet med en frekvens på 500hz.

Vi har fått ut data och skrivit python kod som analyserar punkterna och plottar en kurva utifrån punkterna. Det syns tydligt i kurvan hur luftmotståndet "agerar kvadratiskt" i början för att sedan påverka rörelsen linjärt när hastigheten har sjunkit.

Men det jag har problem med att förstå är hur jag utifrån det ska kunna få fram luftmotståndkoefficienten. Jag gissar att jag kan göra en regressionsanalys på kurvan för att fram dämpningenen men samtidigt, då får jag ju fram luftmotståndet och inte luftmotståndkoefficienten?

Ytterligare har jag svårt att förstå hur luftmotståndkoefficienten inte beror på hastigheten. Det ända jag har kunnat hitta som visar på att det inte beror på hastigheten är om man använder Stokes Lag och sätter in det i luftmotståndsformeln fast för en låg hastighet (alltså linjärt beroende). Men som jag förstår så kan man bara använda Stokes Lag om det är en punkt massa? Så då skulle det inte funka för andra former som t.ex cylindrar, men ändå så finns det på wikipedia fasta värden på luftmotståndkoefficienten??

Tack på förhand!

Koefficienten är formberoende, ja. Värden på Wikipedia bör vara för en given form (tvärsnitt relativt flödesriktning). Den är också hastighetsberoende.

För att få fram koefficienten gör ni en ansats och linjäriserar om nödvändigt.

Du har varit sparsmakad i att ange resultat från experimentet. Men, sannolikt är er uppställning sådan att det existerar två olika regimer:

$F_{luft,kvad} = k_{kvad}\cdot v^2$

$F_{luft,linj} = k_{linj} \cdot v$

Ni ska bestämma $k_{kvad}$ och $k_{linj}$ . Anpassa en kurva med regressionsanalys eller dylikt och ta fram faktorn.

Sedan fås luftmotståndskoefficienten $C_d$ från hur den relaterar till $k$ , men det får ni lista ut.

KorrAtara skrev:

Det syns tydligt i kurvan hur luftmotståndet "agerar kvadratiskt" i början för att sedan påverka rörelsen linjärt när hastigheten har sjunkit.

Hur kan du se det? På den harmoniska dämpningen? Den följer något slags exponentiellt avtagande envelopp:

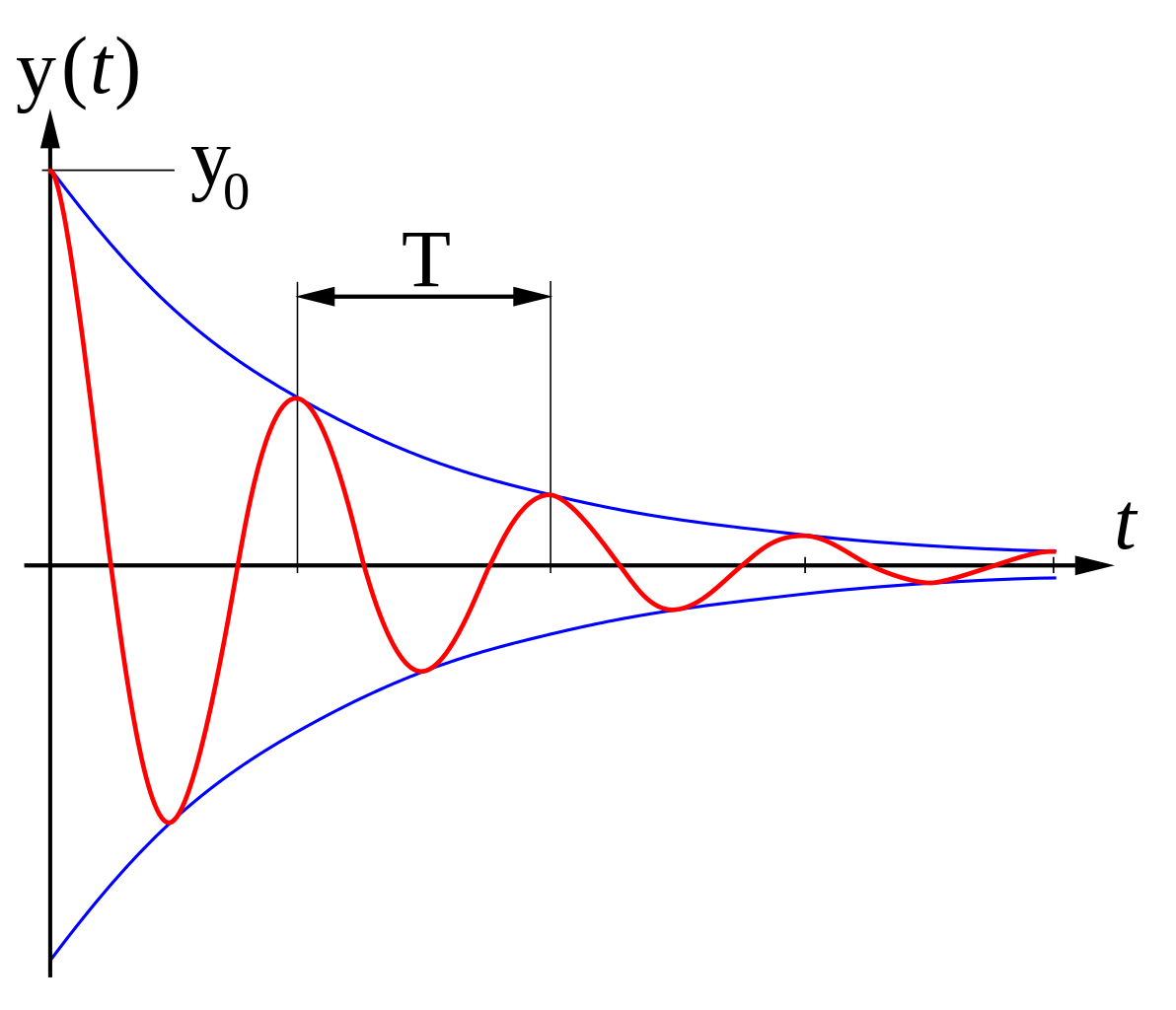
Det kan lätt misstas för att vara kvadratiskt följt av linjärt. Oavsett får du gärna visa vad du menar. Det brukar inte gå att tyda kurvor över $F(v)$ för en plan pendel särskilt enkelt utan massvis av arbete.

Förslag till ansats

Nedan är rörelseekvationen för en plan pendel där vinkeln relativt vertikalen är koordinat:

$I\overset{..}{\theta} + (\kappa _1 \left|\dot{\theta}\right|+\kappa_2)\dot{\theta}+mgL \sin\left(\theta\right)=0$

Där $L$ är längden på pendeln, $\theta$ är vinkeln från vertikalen samt $\kappa_1$ och $\kappa_2$ är koefficienter för vinkelhastighet i kvadratiska respektive linjära regimen.

Hastighet och position

Ni kan alltid relatera vinkel och vinkelhastighet till position respektive tangentiell hastighet genom geometri.

Lösning

Denna differentialekvation styr mekaniken och är vad ni modellerar mot er data, och den kan lösas numeriskt. Med startgissning på koefficienterna kan ni använda en optimeringssnurra som använder minstakvadratmetod eller liknande för att anpassa en numerisk lösning och bestämma koefficienterna.

Hej SaintVenant!
Den föreslagna ansatsen har jag sett innan. Men det jag inte förstår riktigt med den är. Vi har ju alla parametrar förutom kappa. Sedan har vi en kurva som ser ungefär likadan ut som den du skickade. Jag förstår bara inte, om modellera den ekvationen mot vår data för att få ut kappa värdena. Vad är det egentligen kappa betyder, för det är bara ett mått på dämpningen.

Jag har med lite research nu försökt att förstå mig på vad kopplingen är mellan kappa och C_d. Tycker bara att det låter lite konstigt att man kan göra följden beräkningar.

v=Lθ(prick) --> F_drag = 1/2ρCdAL^2θ(prick)^2
τ_drag=L⋅F_drag=L⋅1/2ρCdAL^2θ(prick)^2
L⋅1/2ρCdAL^2θ(prick)^2 = κ_1 θ(prick)^2

och sedan lösa för C_d. Tycker det känns fel att göra så, känns fel att isolera den kvadratiska termen..

Aja här har jag kört fast. Jag kan uppdatera lite med grafer om det önskas. Och tack för svaret!

Du isolerar den över en regim. Alltså, ett intervall av hastighet.

Men mitt nya förslag är att du skippar det.

Håll det simpelt

För att göra allt detta enklare skulle jag utgå helt från att klassiska ekvationen gäller där $F_{drag}\propto v^2$ . Alltså inget linjärt beteende, ingen linjär regim. Samt att $C_d$ är konstant. Speciellt eftersom det normalt bara är vid väldigt låga hastigheter som linjärt råder och stora skillnader i hastighet som variation av $C_d$ kan skönjas.

Studera sedan hur väl detta modellerar er data. Glöm inte att det är målet med hela uppgiften; att hitta en anpassning byggd av parametrar som följer er data väl.

Nämnd beräkning

Det är inget konstigt med den beräkningen. Det är så de relaterar till varandra. Alltså innehåller kappa i detta fall massa kända konstanter så som fluiddensitet, volym etc. utöver $C_d$ .

Men du kan gärna visa lite kring hur långt ni kommit eller ställa fler frågor.

Fråga om status

Har ni löst differentialekvationen numeriskt och anpassat den till er data?

Svara

Visa senaste svar