Numerisk beräkning av egenvärden - Linjär Algebra (KG. Andersson)

Nu blev det helt plötsligt väldigt invecklat i kapitlet om egenvärden och egenvektorer. Jag har kört fast på det här delkapitlet och vet inte hur jag ska lösa uppgifterna, avsaknaden av exempeluppgifter gör det inte direkt enklare...

Jag kan väl börja med den här frågan:

Talen a_k och b_k definieras för k ≥ 0 av

$\{\begin{cases} a_{k + 1} \begin{matrix} = & a_{k} + & 2 b_{k} \end{matrix} \\ b_{k + 1} \begin{matrix} = & 2 a_{k} + & b_{k} \end{matrix} \begin{matrix} \end{matrix} \end{cases}$

a₀=3, b₀=1. Beräkna a₁₀ och b₁₀.

Någons slags ledning? När jag tittar i facit ser jag en lösningsform jag inte är bekant med överhuvudtaget, syns inte någonstans i faktadelen dvs. Den är på formen " $a \times b^{k} + c$ " där a, b och c är konstanter, hur löser jag det här?! TIA

Denna fråga är en övning i att omvandla rekursiva formler med hjälp av matriser. Vi kan skriva de första två värdena, $a_0$ och $b_0$ , som en vektor: $[\begin{matrix} a_{0} \\ b_{0} \end{matrix}]$ . Eftersom $a_1$ och $b_1$ är linjärkombinationer av $a_0$ och $b_0$ kan vi skriva dem som $[\begin{matrix} a_{1} \\ b_{1} \end{matrix}] = [\begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix}] \cdot [\begin{matrix} a_{0} \\ b_{0} \end{matrix}]$ . På samma sätt kan vi skriva en mer allmän formel: $[\begin{matrix} a_{k + 1} \\ b_{k + 1} \end{matrix}] = [\begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix}] \cdot [\begin{matrix} a_{k} \\ b_{k} \end{matrix}]; [\begin{matrix} a_{0} \\ b_{0} \end{matrix}] = [\begin{matrix} 3 \\ 1 \end{matrix}]$ .

Om vi vill beräknaden tionde iterationen av formeln blir det därför $[\begin{matrix} a_{10} \\ b_{10} \end{matrix}] = {[\begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix}]}^{10} \cdot [\begin{matrix} 3 \\ 1 \end{matrix}]$ . Vad kan vi göra nu? :)

Smutstvätt skrev:
Denna fråga är en övning i att omvandla rekursiva formler med hjälp av matriser. Vi kan skriva de första två värdena, $a_0$ och $b_0$ , som en vektor: $[\begin{matrix} a_{0} \\ b_{0} \end{matrix}]$ . Eftersom $a_1$ och $b_1$ är linjärkombinationer av $a_0$ och $b_0$ kan vi skriva dem som $[\begin{matrix} a_{1} \\ b_{1} \end{matrix}] = [\begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix}] \cdot [\begin{matrix} a_{0} \\ b_{0} \end{matrix}]$ . På samma sätt kan vi skriva en mer allmän formel: $[\begin{matrix} a_{k + 1} \\ b_{k + 1} \end{matrix}] = [\begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix}] \cdot [\begin{matrix} a_{k} \\ b_{k} \end{matrix}]; [\begin{matrix} a_{0} \\ b_{0} \end{matrix}] = [\begin{matrix} 3 \\ 1 \end{matrix}]$ .

Om vi vill beräknaden tionde iterationen av formeln blir det därför $[\begin{matrix} a_{10} \\ b_{10} \end{matrix}] = {[\begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix}]}^{10} \cdot [\begin{matrix} 3 \\ 1 \end{matrix}]$ . Vad kan vi göra nu? :)

Tack Smutstvätt! Jag kan ju lösa den där matrisekvationen relativt enkelt genom multiplikation, men osäker på hur jag får det på den formen som jag skrev om i ursprungsfrågan.

Smutstvätt skrev:
Denna fråga är en övning i att omvandla rekursiva formler med hjälp av matriser. Vi kan skriva de första två värdena, $a_0$ och $b_0$ , som en vektor: $[\begin{matrix} a_{0} \\ b_{0} \end{matrix}]$ . Eftersom $a_1$ och $b_1$ är linjärkombinationer av $a_0$ och $b_0$ kan vi skriva dem som $[\begin{matrix} a_{1} \\ b_{1} \end{matrix}] = [\begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix}] \cdot [\begin{matrix} a_{0} \\ b_{0} \end{matrix}]$ . På samma sätt kan vi skriva en mer allmän formel: $[\begin{matrix} a_{k + 1} \\ b_{k + 1} \end{matrix}] = [\begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix}] \cdot [\begin{matrix} a_{k} \\ b_{k} \end{matrix}]; [\begin{matrix} a_{0} \\ b_{0} \end{matrix}] = [\begin{matrix} 3 \\ 1 \end{matrix}]$ .

Om vi vill beräknaden tionde iterationen av formeln blir det därför $[\begin{matrix} a_{10} \\ b_{10} \end{matrix}] = {[\begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix}]}^{10} \cdot [\begin{matrix} 3 \\ 1 \end{matrix}]$ . Vad kan vi göra nu? :)

Såhär ser min lösning ut, men tänker att det borde finnas något mer allmänt sätt att svara, då det här skulle bli svårt att beräkna om k är väldigt stort (för övrigt vet jag att ekvivalenspilarna är lite lustiga på sina ställen).

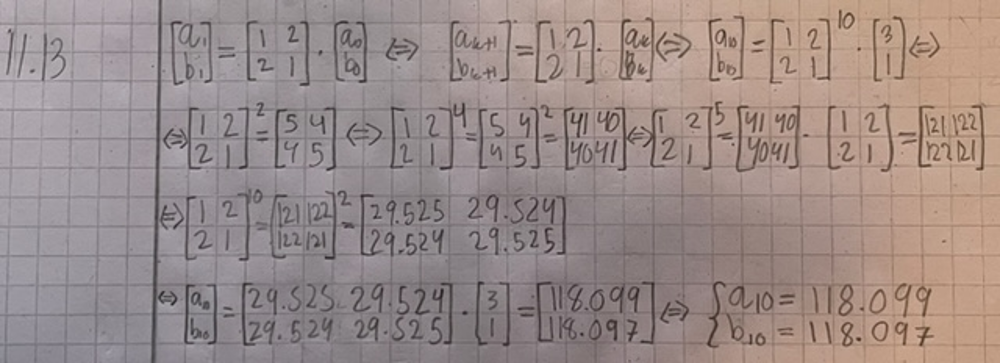
Det går att göra detta på ett mycket enklare sätt, om vi diagonaliserar matrisen får vi att matrisen $[\begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix}]$ kan skrivas som:

$[\begin{matrix} - 1 & 1 \\ 1 & 1 \end{matrix}] [\begin{matrix} - 1 & 0 \\ 0 & 3 \end{matrix}] (\frac{1}{2} [\begin{matrix} - 1 & 1 \\ 1 & 1 \end{matrix}])$

Och då är matrisen upphöjd till tio lika med $[\begin{matrix} - 1 & 1 \\ 1 & 1 \end{matrix}] {[\begin{matrix} - 1 & 0 \\ 0 & 3 \end{matrix}]}^{10} (\frac{1}{2} [\begin{matrix} - 1 & 1 \\ 1 & 1 \end{matrix}]) = . . .$ :)

Smutstvätt skrev:
Det går att göra detta på ett mycket enklare sätt, om vi diagonaliserar matrisen får vi att matrisen $[\begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix}]$ kan skrivas som:

$[\begin{matrix} - 1 & 1 \\ 1 & 1 \end{matrix}] [\begin{matrix} - 1 & 0 \\ 0 & 3 \end{matrix}] (\frac{1}{2} [\begin{matrix} - 1 & 1 \\ 1 & 1 \end{matrix}])$

Och då är matrisen upphöjd till tio lika med $[\begin{matrix} - 1 & 1 \\ 1 & 1 \end{matrix}] {[\begin{matrix} - 1 & 0 \\ 0 & 3 \end{matrix}]}^{10} (\frac{1}{2} [\begin{matrix} - 1 & 1 \\ 1 & 1 \end{matrix}]) = . . .$ :)

Ja såklart, diagonalisering! Stort tack.

Varsågod! :)

Svara

Visa senaste svar