Visa spoiler
Skriv ditt dolda innehåll här
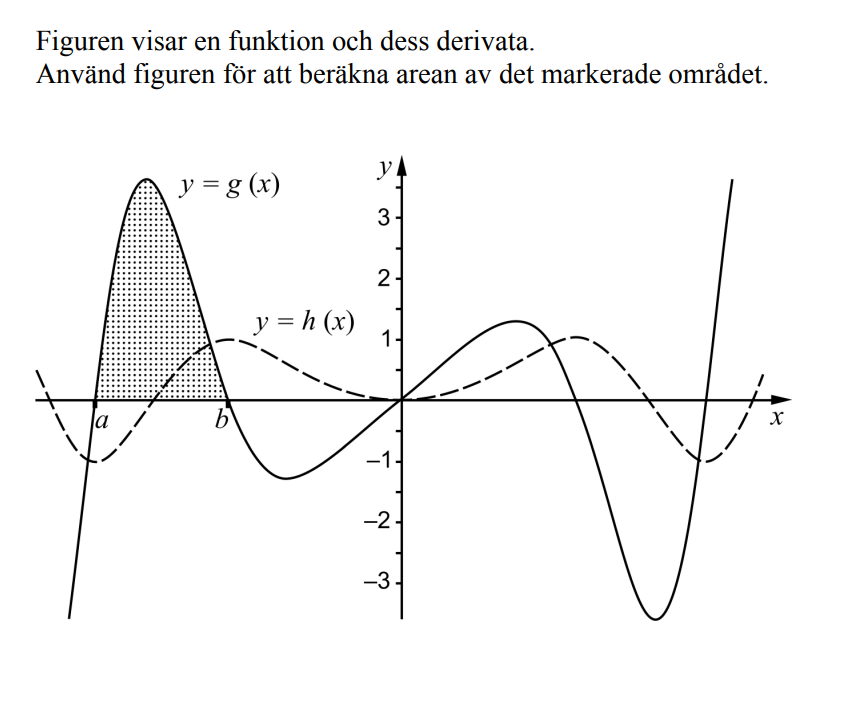
Hur ska man förklara att h(x) är derivata till g(x)? När man beräknar integralen, bestämmer man primitiva funktionen först sen sätter in h(a) - h(b).
AMGOP skrev:Visa spoiler
Hur ska man förklara att h(x) är derivata till g(x)? När man beräknar integralen, bestämmer man primitiva funktionen först sen sätter in h(a) - h(b).
Vi kan se att den är derivata exempelvis eftersom ställena där h skär x-axeln har g extrempunkter.
Detta är fel.
AlexMu skrev:AMGOP skrev:Visa spoiler
Hur ska man förklara att h(x) är derivata till g(x)? När man beräknar integralen, bestämmer man primitiva funktionen först sen sätter in h(a) - h(b).
Vi kan se att den är derivata exempelvis eftersom ställena där h skär x-axeln har g extrempunkter.
Men varför ska man beräkna h(a)-h(b) och inte H(a)-H(b), alltså primitiva funktionen?
AMGOP skrev:AlexMu skrev:AMGOP skrev:Visa spoiler
Hur ska man förklara att h(x) är derivata till g(x)? När man beräknar integralen, bestämmer man primitiva funktionen först sen sätter in h(a) - h(b).
Vi kan se att den är derivata exempelvis eftersom ställena där h skär x-axeln har g extrempunkter.
Men varför ska man beräkna h(a)-h(b) och inte H(a)-H(b), alltså primitiva funktionen?
h är prim.fkn. till g
Trinity2 skrev:AMGOP skrev:AlexMu skrev:AMGOP skrev:Visa spoiler
Hur ska man förklara att h(x) är derivata till g(x)? När man beräknar integralen, bestämmer man primitiva funktionen först sen sätter in h(a) - h(b).
Vi kan se att den är derivata exempelvis eftersom ställena där h skär x-axeln har g extrempunkter.
Men varför ska man beräkna h(a)-h(b) och inte H(a)-H(b), alltså primitiva funktionen?
h är prim.fkn. till g
Hur? Uppgiften säger att "en funktion och dess derivata"
Ja, antingen är g derivatan av h eller så är h derivatan av g.
