Normalytintegral
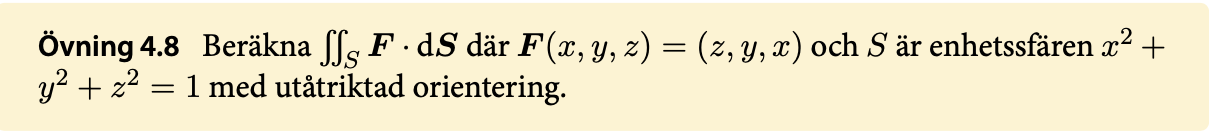
1. Detta är en normalytintegral om jag förstår det rätt. Jag har svårt att förstå vad det är för något, rent konceptuellt. Någon som kan förklara så att en femåring förstår vad en normalytintegral är?
2. Hur gör man för att räkna ut uppgiften?
Jag har kommit så långt att jag parametriserat området, genom att byta till sfäriska koordinater och "tagit bort" variabeln r eftersom den är konstant 1. Då har jag bara två vinklar kvar som variabler, theta och phi, som båda går från 0 till 2pi.
Den här uppgiften blir väldigt enkel med Gauss sats, har ni gått igenom den? Annars får du beräkna integralen.
Båda vinklarna kan inte gå från 0 till 2π, då täcker du in "baksidan" en gång för mycket.
Med z=rcos(θ) är t.ex. rcos(2π/3)=rcos(4π/3)=-0.5r
En normalytintegral är helt enkelt fältets normalkomponent på ytan som integreras. Man plockar ut normalkomponenten genom att bilda skalärprodukten mellan ytans normal och fältet. Sedan samlar man ihop (integrerar) normalkomponenten över hela ytan
Uttryck fältet i θ och ϕ. Det gör du genom att helt enkelt substituera x,y,z i fältet.
F(r,θ,φ)=?
Vad blir det vektoriella ytelementet för en sfär?
dS=?
Bilda skalärprodukten F·dS och ställ upp ytintegralen.
Den här uppgiften blir väldigt enkel med Gauss sats, har ni gått igenom den?
Den har nämnts, men har inte fattat vad den betyder eller hur den används. Har inte fått se exempel på den.
Båda vinklarna kan inte gå från 0 till 2π, då täcker du in "baksidan" en gång för mycket.
Hm okej. Går en av dom bara från 0 till pi då?
En normalytintegral är helt enkelt fältets normalkomponent på ytan som integreras. Man plockar ut normalkomponenten genom att bilda skalärprodukten mellan ytans normal och fältet. Sedan samlar man ihop (integrerar) normalkomponenten över hela ytan
Ja, det är ungefär så det står i vår kurslitteratur också. Jag har svårt att fatta vad det är. Om man skulle förklara detta till exempel för sin mamma, som inte ens vet vad en andragradsekvation är för något, hur hade man gjort då?
Uttryck fältet i θθ och ϕϕ. Det gör du genom att helt enkelt substituera x,y,zx,y,z i fältet.
Såhär?
Vad blir det vektoriella ytelementet för en sfär?
Ingen aning? Är det den man multiplicerar integranden med när man byter till polära koordinater? Isåfall typ r^2sin^2(theta) eller något liknande?
Jag tror tyvärr du måste släppa att en femåring ska kunna förstå vad en normalytintegral är på ett meningsfullt sätt.
Ett vektorfält är något som tilldelar varje punkt i rummet en vektor.
I punkten (x=1,y=0,z=0) är t.ex. vektorfältet i vår uppgift F=(0,0,1). Det är en vektor som pekar rakt upp i z-led.
Den utåtriktade enhetsnormalen till sfären pekar i samma punkt rakt ut från sfären i radiell led. Det blir i det här fallet i x-led
ˆn=(x,y,z)√x2+y2+z2=(1,0,0)1
F·ˆn=(0,0,1)·(1,0,0)=0
Normalytintegralen är alltså summan av liknande beräkningar för varenda punkt på hela enhetssfären.
--------------------------------------------------------------------------------------------------------
Om du vill kan du hoppa över sfäriska koordinater och använda symmetriargument enligt följande
F·ˆn=(z,y,x)·(x,y,z)1=y2+2xz≡y2
Eftersom termen xz är ojämn genom xz-planet i det symmetriska integrationsområdet.
Alltså blir integralen
∫Sy2dS=∫2π0∫π0sin2(θ)cos2(φ)
D4NIEL skrev:Jag tror tyvärr du måste släppa att en femåring ska kunna förstå vad en normalytintegral är på ett meningsfullt sätt.
Ett vektorfält är något som tilldelar varje punkt i rummet en vektor.
I punkten (x=1,y=0,z=0) är t.ex. vektorfältet i vår uppgift . Det är en vektor som pekar rakt upp i z-led.
Den utåtriktade enhetsnormalen till sfären pekar i samma punkt rakt ut från sfären i radiell led. Det blir i det här fallet i x-led
Normalytintegralen är alltså summan av liknande beräkningar för varenda punkt på hela enhetssfären.
--------------------------------------------------------------------------------------------------------
Om du vill kan du hoppa över sfäriska koordinater och använda symmetriargument enligt följande
Eftersom termen är ojämn genom xz-planet i det symmetriska integrationsområdet.
Alltså blir integralen
Väntar mig inte att en femåring ska kunna förstå såklart, tänkte bara att det kunde förklaras med enklare begrepp så man förstår konceptet. Förstår att det är svårt att göra, tack iallafall.
Jag vill nog använda sfäriska koordinater, jag vet inte vad symmetriargumentet är för något. Vet inte heller vad som menas med att xz är ojämn, och vet inte vad det likamedstecknet med tre streck betyder. Använde du Gauss sats här?
Vi låter Gauss sats vila tills vidare.
När du infört sfäriska koordinater (med r=1) för enhetssfären) är nästa steg att finna en normal med rätt normering, Det gör du på samma sätt som i uppgiften med normalen till planet, dvs bilda
Du kan också "fuska" och använda
direkt från formelsamlingen.
D4NIEL skrev:Vi låter Gauss sats vila tills vidare.
När du infört sfäriska koordinater (med r=1) för enhetssfären) är nästa steg att finna en normal, Det gör du på samma sätt som i uppgiften med normalen till planet, dvs bilda
Vi får inte använda formelsamlingar i kursen jag läser tyvärr.
Det är en jättejobbig kryssprodukt. Jag gjorde ett försök här:
Vad är det jag fått fram här då?
Det verkar ha smugit sig in ett fel i beräkningen av
och
Alltså blir
Det som nu återstår är att bilda skalärprodukten och beräkna integralen.
Det blir som sagt en del räkningar.
Du kan jämföra det med beräkningen genom Gauss sats
Eller med beräkningen då man håller sig kvar i kartesiska koordinater till efter skalärprodukten mellan ytnormalen och fältet.
D4NIEL skrev:Det verkar ha smugit sig in ett fel i beräkningen av
och
Alltså blir
Det som nu återstår är att bilda skalärprodukten och beräkna integralen.
Det blir som sagt en del räkningar.
Du kan jämföra det med beräkningen genom Gauss sats
Eller med beräkningen då man håller sig kvar i kartesiska koordinater till efter skalärprodukten mellan ytnormalen och fältet.
Ok, ska prova integralen när jag kommer hem.
Så likt den andra uppgiften med tangentplanet är kryssprodukten av de partiella detivatorna normalen som funktion av beror på theta och phi?
D4NIEL skrev:Det verkar ha smugit sig in ett fel i beräkningen av
och
Alltså blir
Det som nu återstår är att bilda skalärprodukten och beräkna integralen.
Det blir som sagt en del räkningar.
Du kan jämföra det med beräkningen genom Gauss sats
Eller med beräkningen då man håller sig kvar i kartesiska koordinater till efter skalärprodukten mellan ytnormalen och fältet.
Ok, det går lite trögt här.
Vi har fått en formel som ser ut såhär:
Jag har ju nu med din hjälp räknat ut r'u x r'v.
Hur gör man för att ställa upp F(r(u,v)) ?
Det är bara att sätta in uttrycken för som funktioner av i fältet
Sedan bildar du skalärprodukten
För att den sista integralen inte ska bli för jobbig måste man tänka igenom vilka trigonometriska termer som ger bidraget 0 över vissa intervall. T.ex. ger allt som innehåller nollbidrag eftersom
D4NIEL skrev:Det är bara att sätta in uttrycken för som funktioner av i fältet
Sedan bildar du skalärprodukten
För att den sista integralen inte ska bli för jobbig måste man tänka igenom vilka trigonometriska termer som ger bidraget 0 över vissa intervall. T.ex. ger allt som innehåller nollbidrag eftersom
Jag förstår inte hur man sätter in uttrycken för x,y,z som funktioner av r, theta, phi i fältet (z,y,x). Jag förstår inte ens vad det är jag gör.
Jag tittade även igenom min beräkning av r'phi. Jag ser inte vad jag har gjort fel. Är vi överens om att r ser ut såhär?

Ja, det är korrekt. Sfäriska koordinater är
Och med för enhetssfären samt blir det
Deriverar vi partiellt med avseende på måste sista elementet vara 0
Eftersom
Vidare är fältet
Och du behöver finna skalärprodukten
D4NIEL skrev:Den här uppgiften blir väldigt enkel med Gauss sats, har ni gått igenom den? Annars får du beräkna integralen.
Hur löser man detta med Gauss sats förresten? Rent slarvigt sagt trodde jag Gauss beräknade flödesintegral genom en yta genom att beräkna volymen av kroppen som begränsas av samma yta. Men här verkar man vilja ha ytintegral och inte flödesintegral, eller har jag fel?
Det är samma sak. En ytintegral är flödet genom ytan i enhetsnormalens riktning. Flödesintegralen är en normalytintegral.
Gauss sats säger att man kan relatera det totala flödet av ett vektorfält ut genom en sluten yta med den sammanlagda divergensen av fältet i den inneslutna volymen.
Det är alltså en normalytintegral (flödet genom ytan, flödesintegral) över ytan som omvandlas till en volymsintegral över den inneslutna volymen .
I det här fallet blir det särskilt lätt eftersom (divergensen av F är 1)
Integralen reduceras därmed till volymen av enhetssfären.
D4NIEL skrev:Det är samma sak. En ytintegral är flödet genom ytan i enhetsnormalens riktning. Flödesintegralen är en normalytintegral.
Har inte ens tänkt på detta tidigare. Jag tror jag förvirrade mig själv tidigare med när man arbetar med en skalärfunktion, dvs att F skulle vara en skalärfunktion, för då beräknar man ytintegralen snarlikt, men anpassar efter att det är en skalärfunktion. Däremot när F är vektorfält då motsvarar ytintegralen flödesintegralen/normalytintegralen istället och måste beräknas på sättet som diskuterats i tråden. Tack för insikten!

