normallinjer till grafen
Något tips för hur jag kan lösa denna uppgift? Vet inte hur jag ska börja.
Tänkte att jag skulle kunnat räkna ett uttrycka för de möjliga tangeterna och sedan gör ett uttryck för de linjer som är 1/-k.
Vet hur jag ska räkna ut alla möjliga tangter om jag vet en punkt som den ska gå igenom, men här vet jag ingen punkt för liken tangeten kommer att gå igång.
Om tangeringspunkten är (x , f(x))
så går väl normalen genom denna punkt och (1 , 4)
och har dessutom lutningen -1 / f ' (x) .
Kan du få ihop en ekvation av det?
Här är f(x)= x2 / 2
Arktos skrev:Om tangeringspunkten är (x , f(x))
så går väl normalen genom denna punkt och (1 , 4)
och har dessutom lutningen -1 / f ' (x) .Kan du få ihop en ekvation av det?
Här är f(x)= x2 / 2
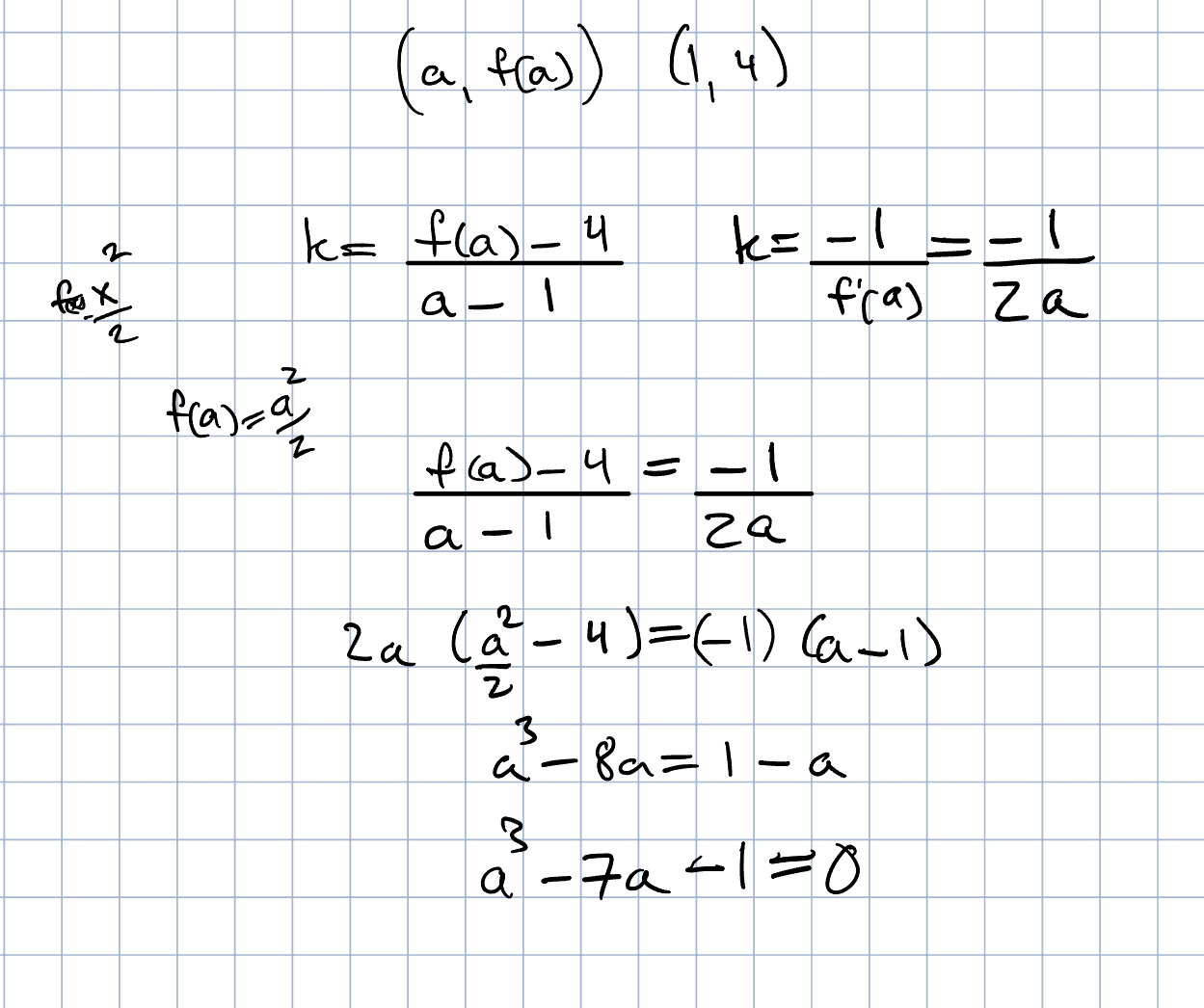
Jag tänker mig att att jag har en punkt (1,4) och en punkt (a,f(a)) sätter ett uttryck för k lutningen mellan punkten. Och samma lutning som blir -1/f'(a)= -1/2a.
Sedan sätter jag dessa uttryck lika med varrandra. För hoppningen var att kunna få ut ett värde till ekvationen för att du ge mig värdet a, men jag att rationella rötter saknas.
OBS att f '(x) inte är lika med 2x
Arktos skrev:OBS att f '(x) inte är lika med 2x
Ok tack! Ser dock ut som att jag får en ekvation som saknar rationella rötter ändå
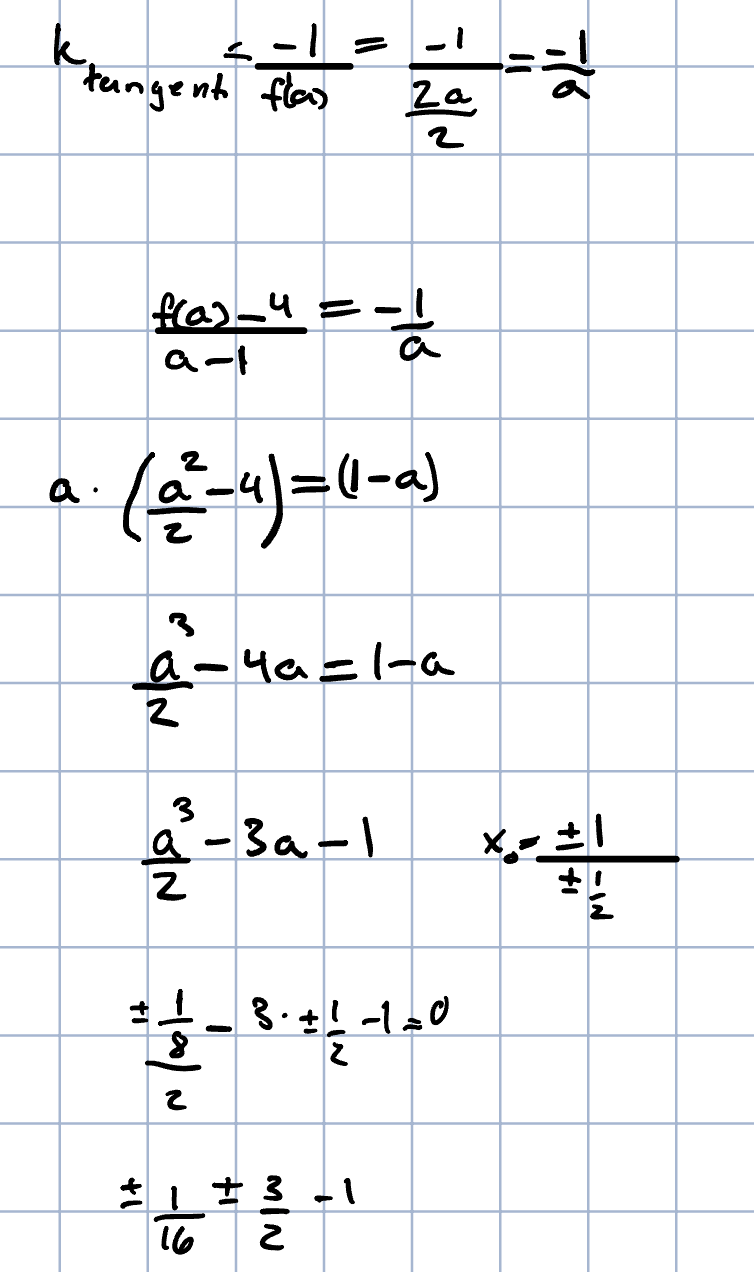
Rationella rötter är väl inte nödvändigt.
Det räcker med reella rötter, åtminstone en.
Och varje tredjegradspolynom har minst ett reellt nollställe.
Jag får samma ekvation som du:
a3 – 6a – 2 = 0
Arktos skrev:Rationella rötter är väl inte nödvändigt.
Det räcker med reella rötter, åtminstone en.
Och varje tredjegradspolynom har minst ett reellt nollställe.Jag får samma ekvation som du:
a3 – 6a – 2 = 0
Jag kommer inte vidare här ifrån. Kan du hjälpa mig få ut ett värde på a?
När jag väl har fått ut en värde på a så tänker jag att det bara är att sätta in det i ekvationen för normalen, så ska uppgiften vara löst?
Hur är det tänkt att du ska lösa ekvationen?
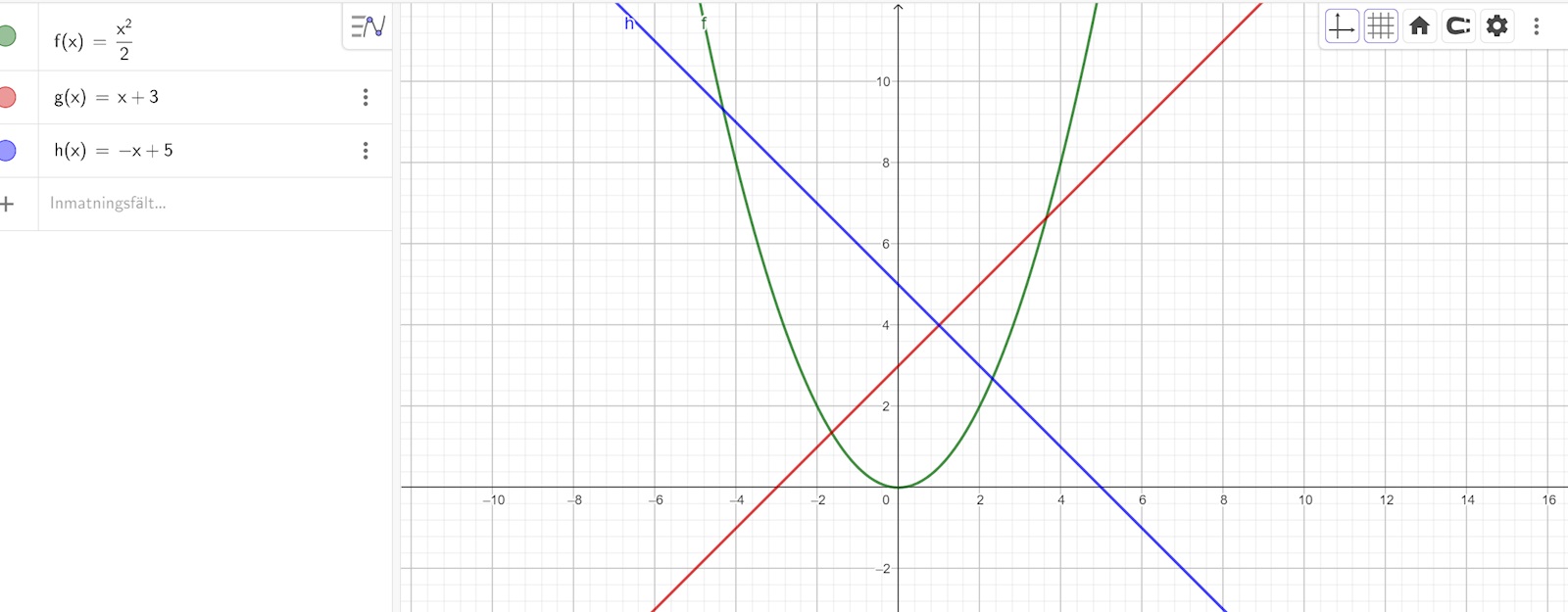
Av din figur att döma bör det finnas tre normales som går genom (1 , 4).
Rita tredjegradspolynomet och f(x) i samma koordinatsystem
och se om inte det verkar stämma, dvs att ekv har tre reella rötter.
Arktos skrev:Hur är det tänkt att du ska lösa ekvationen?
Av din figur att döma bör det finnas tre normales som går genom (1 , 4).
Rita tredjegradspolynomet och f(x) i samma koordinatsystem
och se om inte det verkar stämma, dvs att ekv har tre reella rötter.
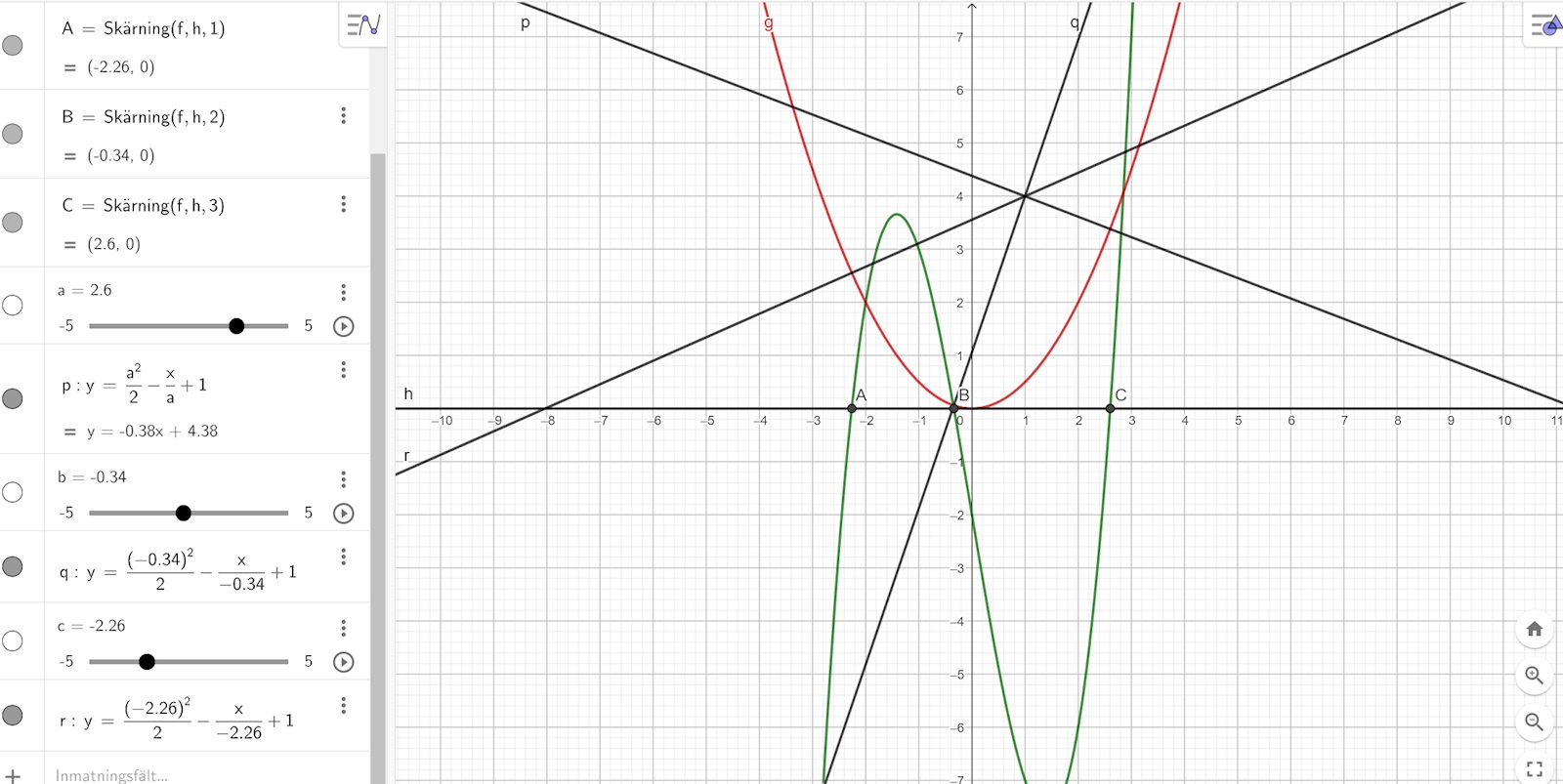
På bilden syns det att lösningarna till tredjegradspolynomet blev: -2.26; -0.34; 2.6
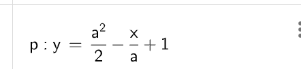Fick detta som normalens ekvation då jag förenklade. Det hela ser ut att stämma när jag kollar på grafen.
Fråga: Jag får inte hur jag skulle kunnat räkna ut -2.26; -0.34; 2.6 utan grafräknare. Detta var en tenta fråga, finns dock inget facit.
Snyggt. Jag gjorde som du.
Ritade i Desmos. Den geometriska bilden är ju övertygande.
[Jag förstår inte din ekvation för normalen. Hur fick du fram den?]
Lät sedan Mathematica lösa ekvationen och fick tre väldigt komplexa rötter.
Konstigt – minst en borde ju ha varit reell
Numeriskt hade hade dock alla tre försvinnande små imaginärdelar.
(Mma kan inte ge exakta rötter för alla ekv av grad 3 eller högre)
Numerisk lösning bekräftade detta - fick tre reella rötter
lika med de numeriska realdelarna av de komplexa rötterna.
{{a -> -2.2618}, {a -> -0.339877}, {a -> 2.60168}}
Hur skulle man annars ha gjort?
Använda Cardanos formler för lösning av en allmän tredjegradare?
Har du träffat på dem?
Eller finns det något specialtrix för just denna funktion?
Jag misstänker att det är tänkt att punkten ska vara istället för och att man rättade det under tentan.
Tack för tipset!
Värt att prova.
