Normallinje i 3D

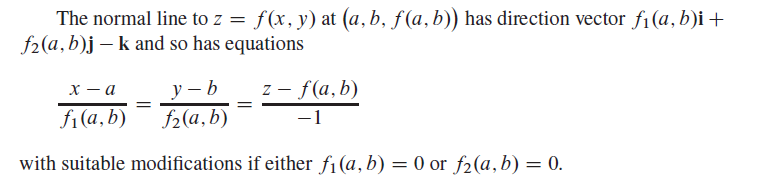
Du har z = f(x, y)

Jag ser det så här

skriv

0 = f(x,y) – z

Det är en nivåyta till 

w = f(x,y) – z

dvs för varje värde på w så beskriver punkterna i högerledet en svävande duk i xyz-rymden.

Den duken har normalvektor (df/dx, df/dy, df/dz) = (f₁ , f₂ , –1) i punkten (a, b, f(a,b)).

Jag är inte hundra på att det är helt stringent, men det förklarar –1 i z-komposanten så att jag kan sova lugnt.

De har ansatt linjen

$(x,y,z)=\mathbf{P}_0+t\mathbf{n}$

Punkten $\mathbf{P}_0$ är $\mathbf{P}_0=(a,b,f(a,b))$ och riktningsvektorn för linjen (normalen) har de normerat så att z-komponenten är $-1$, dvs $(f_1,f_2,-1)$. De har alltså valt en av två möjliga riktningar på normalen och dessutom valt dess längd.

$\begin{pmatrix}x \\ y \\ x\end{pmatrix}=\begin{pmatrix}a \\b \\f(a,b)\end{pmatrix}+t\begin{pmatrix}f_1\\f_2\\ -1\end{pmatrix}$

Löser man ut t i x-, y- och z-led samt tecknar det på parameterfri form $(t=t=t)$ får man

$\displaystyle \frac{x-a}{f_1}=\frac{y-b}{f_2}=\frac{z-f(a,b)}{-1}$

Tack Daniel, din förklaring känns något stringentare än min.