Normalfördelning

Hmmm, det var märkligt, denna typ av uppgift kräver antingen en särskild tabell, eller kunskaper från Ma4. Om frågan hade varit 

Hur många räkor behöver han fånga för att få 500 räkor som väger 16 g eller mer?

vet du hur du skulle löst den frågan? :)

Vad konstigt. För det där är en E uppgift. Kan ju vara så att det blev fel när dom skrev uppgiften! 

Men de  2,3% längst ut motsvarar ju allt som är 16 och över. Kom inte längre än så...

Absolut! Det finns normalfördelningskurvor som tar hänsyn till halva standardavvikelser, de är bara en internetsökning bort, men det är ovanligt att uppgifter förväntar sig att läsaren ska använda sådana. 

Utmärkt början! Så, om du fångar x räkor, är 2,3% av dessa över 16 g. Vad är x, om 2,3% av x ska vara minst 500? :)

Men det borde väll bli 500/2,3 = 217,3913... => 217,3913... • 100 = 21739,13... ?

Ja 🙌🏽 Hur gör jag sen? 

Ingenting, du är klar! Om Roger fångar 21739 räkor kan han räkna med att minst femhundra av dessa väger över 16 gram. :)

Jag fattar. Men tänkte ifall detta kunde hjälpa mig att lösa den ursprungliga uppgiften. För jag skulle ju trots allt ta reda på hur många räkor som måste fångas för att minst 500 ska vara 15g eller mer. 😅 Men det kanske är för överkurs 

Då behöver du en normalfördelningskurva med halva standardavvikelser:

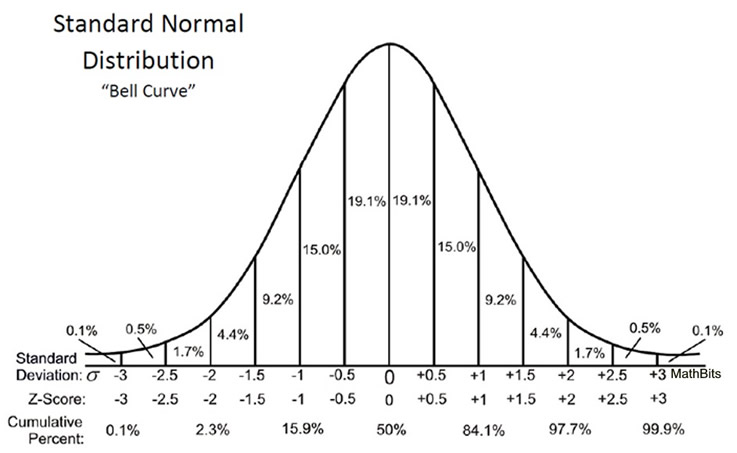
15 gram är 1,5 standardavvikelser. Hur stor andel ligger över 1,5 standardavvikelser? :)

Men är standardavvikelsen på den där kurvan 1 då?

Nja, standardavvikelsens storlek här är inte angiven. "+1.5" betyder +1,5 standardavvikelser. :)

Jaha, okej. Men det kanske är irrelevant så vi struntar i det. 

Men om alla över 16g motsvarade 2,3%, så borde ju det vara 0,1+0,5+1,7=2,3% om vi tittar från höger. Så om vi då ska ta 15 g istället för 16g så borde jag väll addera 2,3% med 4,4% (för det motsvarar 15 g) och då blir det totalt 6,7%?

Japp! :D

Och det blir då 500/6,7 = 74,626865.... => 74,626865....•100=7462,6865.... ~7460

Helt rätt! :D